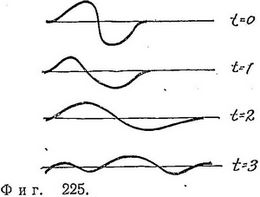
До сих пор мы рассматривали импульсы (небольшие возвышения), равномерно движущиеся вдоль линии. Мы определили среду без дисперсии как среду, в которой волна, имевшая произвольную форму при t=0, движется с постоянной скоростью и сохраняет при этом свою первоначальную форму. При движении через диспергирующую среду (т. е. через среду, обладающую дисперсией) форма волны будет изменяться со временем (фиг. 225).

Спрашивается: нет ли таких форм, которые сохраняются независимо от того, является ли однородная среда диспергирующей или нет? Иными словами, нет ли таких функций положения, которые не изменяют со временем свою форму в случае диспергирующей среды? Оказывается, что есть. Свойства таких волновых форм настолько важны, что мы потратим сейчас немного времени на их изучение.

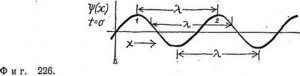
Рассмотрим волну, или волновую функцию, изображенную на фиг. 226 и состоящую из такого регулярного набора возвышений и впадин, что расстояние от возвышения до возвышения остается всегда постоянным, как и расстояние от впадины до впадины или расстояние от любой точки, отвечающей заданной высоте и наклону кривой, до следующей точки такой же высоты и наклона. Это характерное расстояние, на котором форма волны повторяется, называется длиной волны λ. Аналитически такую периодическую волну, обладающую необходимым свойством гладкости, можно записать в виде:

Знать свойства синусов и косинусов не обязательно, однако для тех, кто их знает, отметим, что функция синус принимает одно и то же значение для всех значений х, при которых выражение в круглых скобках кратно 2π, т. е. когда х кратно λ.

Одно из свойств подобной периодической волны состоит в том, что если мы взглянем на нее через некоторое определенное время, необходимое для прохождения волной расстояния λ, то мы заметим, что максимум (возвышение), который мы вначале пометили цифрой 1 (фиг. 226), будет находиться на месте максимума, помеченного вначале цифрой 2. Другое же возвышение, предшествовавшее возвышению 1 и не представленное на графике, займет к этому времени первоначальное место максимума 1. В результате форма волны в этот момент в точности совпадет с той формой, которую она имела при t=0. Мы называем этот характерный отрезок времени τ периодом волны. Отсюда, зная пройденное волной расстояние λ и соответствующий интервал времени τ, можно ввести естественное определение скорости волны:

v = λ/τ (17.3)

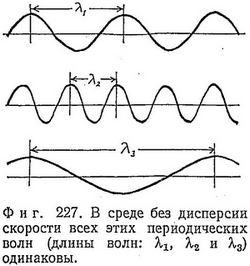
Определим среду без дисперсии как среду, в которой скорость всех таких волн одинакова и не зависит от их длин волн (фиг. 227).

Периодическая волновая функция может быть записана в виде:

Рассматривая ее как функцию х при t фиксированном мы видим, что величина (2π/λ)х+(2π/τ)t возрастает на 2π при увеличении х на длину волны λ. Так, например:

Изменение аргумента синуса на 2π дает первоначальную форму функции (фиг. 228). Точно так же увеличение t на период τ (при фиксированном х) не изменяет первоначальной формы функции.

Введем теперь еще один термин, который не является обязательным, но часто используется и поэтому заслуживает того, чтобы его определить. Это частота волны, которую мы определим следующим образом:

Определение. Частота = 1/период:

v = 1/τ (17.6)

Смысл частоты таков: если зафиксировать свое положение в пространстве, то за 1 с мимо нас пройдет такое количество максимумов, которое численно равно частоте. Следовательно, соотношение:

υ = λ/τ (17.7)

можно записать в иной форме, которая обычно и используется на практике:

υ = λv

Мы описываем периодические синусоидальные или косинусоидальные волны так подробно потому, что они сохраняют свою форму в любой среде. В тех средах, где периодические волны с разными длинами волн распространяются с различными скоростями (диспергирующие среды), любые иные волны изменяют со временем свою форму. В тех же особых средах (например, в вакууме), где периодические волны с любыми длинами волн распространяются с одной и той же скоростью (среды, не обладающие дисперсией), любая произвольная волна сохраняет свою форму.

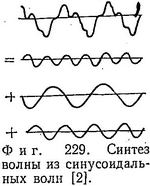
Синусоидальные (или косинусоидальные) волны играют важную роль еще и потому, что существует теорема, согласно которой волна произвольной формы может быть представлена в виде суммы таких синусоидальных волн, как показано на фиг. 229. Эта теорема вместе с принципом суперпозиции часто дает нам возможность найти любое требуемое решение волнового уравнения в виде суммы периодических функций. Из теоремы нам известно, что любая функция представляется в виде суммы периодических функций. Далее, все периодические функции являются, как правило, возможными решениями волнового уравнения. Таким образом, математический анализ волн обычно проводится путем разбиения волны на периодические функции, тогда исследование чрезвычайно упрощается и его результаты легко понять. После этого легко волну произвольной формы снова сконструировать как сумму простых периодических функций.