Иоганн Кеплер, родившийся в 1571 г., был полной противоположностью Браге. Браге был наблюдателем, собиравшим данные и фиксировавшим все, что он видел. Кеплер же был теоретиком, увлеченным мощью математики; подобно Пифагору, он испытывал благоговение перед числами и был зачарован головоломками, относящимися к числам и размерам. После изучения астрономии Кеплер загорелся желанием найти такую математическую схему, которая описывала бы движения планет. Он говорил: «Я отдавал всю энергию своего ума размышлению над этой проблемой». Он посвятил большую часть своей жизни анализу составленных Браге таблиц положений планет, чтобы построить систему кривых, по которым движутся планеты.
Кеплер начал свой многолетний анализ таблиц с исчерпывающего исследования движения Марса. По какой траектории перемещался Марс за время двадцатилетних наблюдений Браге? Была ли эта траектория простой, повторяющейся, чтобы, определив ее однажды, всегда можно было уверенно предсказать положение Марса? Все измерения Брагерыли сделаны, естественно, с Земли. Однако было не ясно, в каком случае траектории планет окажутся проще: если считать, что Земля неподвижна, или, подобно Копернику, полагать, что Земля движется? Кейлер верил, что идея Коперника в основном верна и что Земля вращается вокруг собственной оси, двигаясь одновременно по орбите вокруг Солнца.
Кеплер, как и все до него, начал поиски возможных орбит с различных систем окружностей, движущихся по другим окружностям. Если бы таким путем легко было добиться соответствия с экспериментом, Кеплер скоро достиг бы желаемого результата. Однако поставленная задача оказалась значительно сложнее. Кеплер испробовал бесчисленное количество вариантов, причем каждая попытка была сопряжена с длительными и изнурительными вычислениями. Каждый раз он должен был переводить измеренные Браге углы между планетами и звездами в определенный час ночи в координаты планет в системе, где Солнце неподвижно, а Земля обращается вокруг него.
После примерно 70 попыток построить с помощью системы окружностей траекторию Марса при различных положениях Солнца Кеплеру, наконец, удалось найти такую орбиту, которая довольно хорошо отвечала наблюдениям. Однако вскоре он с ужасом обнаружил, что если продолжить траекторию Марса за те экспериментальные точки, к которым он ее подгонял, то окажется, что она разойдётся с данными наблюдений на 2/15 градуса, т. е. на угол, который пробегает секундная стрелка за 0,02 с. Может быть, ошибся Браге? Может быть, в холодную зимнюю ночь мороз сковал его пальцы или притупил его зрение? Кеплер, который знал методы Браге и его аккуратность, мог положиться на точность его измерений; он заключил, что Браге не мог ошибиться на такую величину, и отверг кривые, которые сам же получил. Вряд ли он смог бы воздать Браге, как наблюдателю, большую честь. И Кеплер не ошибся, потому что Браге оказался прав.
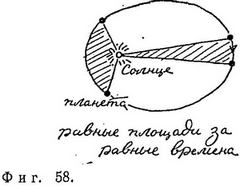
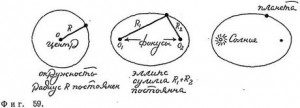
«Эти восемь минут (2/15 градуса) … дадут нам средство преобразовать астрономию», — с этой мыслью Кеплер начал свои поиски заново. Теперь он попытался решить проблему, полагая, что скорость движения планеты по орбите вокруг Солнца переменна, тем самым отвергнув ту древнюю и привычную догму, которая привела Коперника к отказу от системы Птолемея. При своих расчетах Кеплер пользовался воображаемой «спицей колеса», соединяющей Солнце с планетой (с ее помощью ему и удалось сделать свое первое великое открытие). Он обнаружил, что спица движется таким образом, что заметает равные площади за равные промежутки времени (фиг. 58). Сейчас этот вывод называется вторым законом Кеплера. После этого открытия Кеплер окончательно отказался от попыток построить траектории планет с помощью комбинации окружностей и начал пробовать в качестве орбит всевозможные овалы. В результате длительных вычислений он получил свой наиболее важный результат, так называемый первый закон. Кеплер установил, что планеты движутся по эллиптическим орбитам, в одном из фокусов которых находится Солнце (фиг. 59).
После многолетних трудов ему удалось наконец найти те простые траектории, которые согласовывались с известными движениями всех планет. Более того, оказалось, что планеты перемещаются по этим траекториям таким образом, что воображаемые линии, соединяющие их с Солнцем, заметают за равные промежутки времени равные площади.
Затем Кеплер попытался найти связь между размерами орбит и временами полного обращения планет вокруг Солнца, называемыми периодами обращения. Со времен греков полагали, что планеты, имеющие большие орбиты, затрачивают на их полное прохождение большие времена. После множества попыток Кеплер наконец нашел то, что хотел найти: куб радиуса орбиты пропорционален квадрату времени обращения. Случайно обнаружив эту закономерность, Кеплер был поражен той точностью, с которой она выполняется.
В табл. 4 приведены значения этого отношения по данным современных измерений радиуса R и периода Т. Радиус эллиптической орбиты определяется как половина ее большой оси.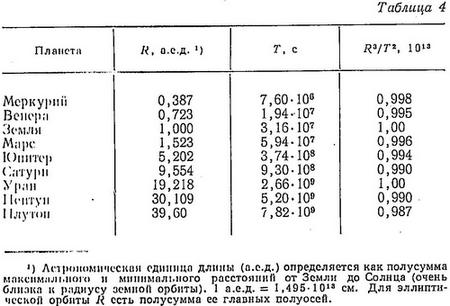
Кеплер был в восторге и не пытался скрывать это:
«То, что шестнадцать лет тому назад я решил искать, ради чего я пришел к Тихо Браге… наконец найдено, и это открытие превзошло все мои самые смелые ожидания… Жребий брошен, книга закончена, и меня не волнует, прочтут ее сейчас или в будущем наши потомки — она может ждать своего читателя в течение столетия, подобно тому как Всевышний ждал наблюдателя своих творений в течение шести тысяч лет».
Вот те три закона Кеплера, которые явились решением проблемы движения планет:
- Каждая планета обращается по эллиптической орбите вокруг Солнца, которое находится в одном из ее фокусов.
- Линия, соединяющая Солнце с планетой, заметает за равные времена равные площади.
- Для всех планет отношение куба радиуса к квадрату периода обращения одинаково:
Эти законы представляли собой выдающееся достижение. Результаты двадцатилетних наблюдений и тысяч измерений оказались сконцентрированными в простой системе кривых и правил. Всякий, кто захотел бы в будущем создать свою систему мира, должен был позаботиться, чтобы она содержала в себе эти три закона, описывающие движения планет. После Кеплера (признанного законодателем небес) возникал только один вопрос: какая из теорий дает правила Кеплера? Что же касается других вопросов, связанных с движением планет, то все они отпали сами собой, так как планеты перестали двигаться равномерно, обращаться по правильным окружностям и соблюдать при движении гармоничные пропорции… Но, возможно, что:
«Есть музыка и в красоте, и беззвучная мелодия, которую играет Купидон, гораздо слаще, чем звук инструмента; потому что музыка имеется во всем, где есть гармония, порядок или пропорция; потому-то мы можем наслаждаться гармонией сфер».