При изучении кинетической теории газов нам удалось отождествить величины, подобные температуре, с чисто механическими величинами — средней кинетической энергией и т. д. Но прежде чем интерпретировать энтропию, следует ввести понятия вероятности и беспорядка (хаотичности). Если считать, что теплота как-то связана сдвижением, то уместно говорить об интенсивности этого движения (скажем, полной энергии) и о том, как это движение распределено (все частицы либо движутся с одной скоростью и в одну сторону, подобно шеренге хорошо вымуштрованных солдат, либо они мечутся во все стороны, как пассажиры на станции метро в час пик). Величину S, названную Клаузиусом энтропией, отождествляют в кинетической теории или статистической механике со степенью хаотичности движения в системе. Энтропия системы мала, когда движение в системе упорядочено или, когда распределение частиц в ней по скоростям и положениям маловероятно. 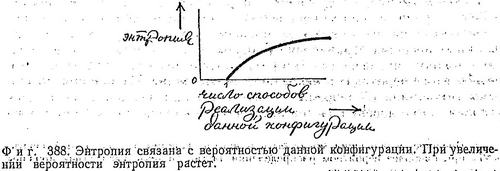 Так, конфигурация частиц, движущихся с одинаковыми: скоростями в одном направлении, имеет очень низкую энтропию. Система, в которой все частицы скопились в одном углу сосуда, тоже обладает малой энтропией. Максимальное же значение энтропии системы соответствует такой конфигурации, которая наиболее вероятна. Качественная зависимость между энтропией и вероятностью состояния имеет вид; показанный на фиг. 388:

энтропия = k_Б*(логарифм числа способов реализации данного распределения с помощью перестановки одинаковых частиц). (27.1)

Из этого определения следует, что энтропия наименее вероятной конфигурации, т. е. конфигурации, которую можно реализовать лишь одним способом, равна нулю, так как:

S = k_Б*логарифм (1) = 0. (27.2)

Таким образом, нам удалось интерпретировать понятие энтропии в терминах понятий механики. Подобно тому как температура, определенная через среднюю кинетическую энергию, обладает всеми макроскопическими свойствами температуры, определенная указанным выше образом энтропия также обладает всеми требуемыми свойствами. С помощью полученного определения можно по-иному сформулировать весьма загадочное второе начало термодинамики, гласящее, что в любом физическом процессе энтропия растет. Теперь можно утверждать, что в любом физическом процессе распределение частиц в системе изменяется от менее вероятного к более вероятному (за исключением особых идеальных случаев, когда распределение не изменяется). Иными словами, в физических процессах упорядоченные системы стремятся стать неупорядоченными. Такая упорядоченная система, как, скажем, фарфоровая ваза, превращается в осколки, если вазу уронить. Рассыпанные осколки вазы сами по себе не могут сложиться нужным образом (это может случиться только в кино, если пустить киноленту в обратную сторону).

Среди следствий из такой интерпретации второго начала имеются и такие, обсуждением которых мы можем развлекаться на досуге. Допустим, что все молекулы, образующие кусок мела, так упорядочили свое движение, что температура мела упала, а он сам неожиданно подпрыгнул перед нашим взором. Вообще говоря, это возможно. Обычно при этом добавляют, что крайне маловероятно; если вычислить вероятность такого события, мы получим, что она равна одной миллиард миллиард…— иными словами, очень маленькой величине. Этим мы можем по крайней мере объяснить тот факт, что мы не наблюдаем такое событие ежедневно.

Но оно может в принципе произойти. Допустим, что такое событие случилось. Скажем, кусок мела неожиданно подпрыгнул сам по себе (фиг. 389). «Поверим» ли мы своим глазам? Иными словами, нас интересует не то, почему мы не наблюдаем такие события, а скорее вопрос: «Захотим ли мы их интерпретировать как статистическую флуктуацию или как иллюзию наших чувств?».