Быть может, наиболее важное свойство потенциальной энергии устанавливается следующей теоремой.
Теорема 12.1. Если силы, действующие на тело, консервативные, то величина работы, затраченной на перемещение его из одной точки в другую, зависит только от положения начальной и конечной точек, или разность потенциальных энергий в двух точках зависит лишь от положения этих точек.
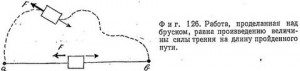
Чтобы оценить важность этой теоремы, рассмотрим случай, когда силы не являются консервативными. В этом случае работа, произведенная над телом, будет зависеть не только от его начального и конечного положений, но и от пути, по которому перемещалось тело. Представим, например, брусок, движущийся с трением по столу. Так как сила трения всегда направлена против движения тела, работа, произведенная над бруском, будет равна величине силы, умноженной на полную длину пути (фиг. 126). Поэтому, если брусок перемещался из точки α в b по прямой, работа будет минимально возможной; если же он перемещался по криволинейному пути, произведенная над ним работа будет больше. Если попытаться определить потенциальную энергию в этом случае, она окажется зависящей не столько от начального и конечного положений тела, сколько от длины пути, пройденного им при перемещении из точки α в точку b. Другими словами, работа, произведенная над телом, будет зависеть от истории его движения, т. е. от того, как оно перемещалось по столу.
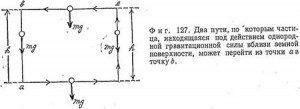
Если хорошенько вдуматься в смысл полученного результата, станет ясно, насколько замечателен тот факт, что все-таки бывают случаи, когда работа, произведенная над телом, оказывается независящей от пути, по которому оно перемещалось, а определяется лишь положением тела в заданный момент. Такие случаи как раз и соответствуют консервативным силам. Проиллюстрируем доказательство, рассмотрев опять движение частицы под действием силы тяжести. Но теперь мы не будем ограничиваться лишь подбрасыванием частицы вверх из точки α до точки b. Представим, что она может двигаться из α в b по любому из нескольких возможных путей. В частности, рассмотрим движение по прямолинейному пути, изученное ранее, и по замкнутому пути, показанному на фиг. 127.
Работа при перемещении частицы из α в b по прямой линии (расстояние между α и b обозначено через h) равна —mgh, как было показано ранее. Вычислим теперь работу вдоль ломаного пути αceb. Этот путь не является совершенно произвольным, но расчет работы вдоль него хорошо поясняет основную идею доказательства. На первом отрезке от α до c сила притяжения перпендикулярна направлению движения тела — ив этом вся суть. Вдоль этого отрезка сила притяжения не совершает никакой работы; этим она в корне отличается от силы трения, которая совершала бы работу вдоль любого отрезка пути. На втором отрезке, от с до е, гравитационная сила направлена против движения и совершает работу, равную —mgh. Наконец, на последнем участке сила притяжения снова перпендикулярна направлению движения тела и не совершает работы. Поэтому работа вдоль всего пути αсеb равна —mgh, как и вдоль прямолинейного пути.
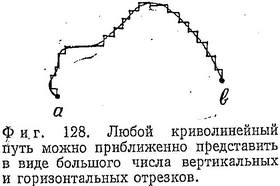
Путь произвольной формы можно разбить на большое число прямолинейных отрезков, каждый из которых будет либо горизонтальным, либо вертикальным (фиг. 128). Работа вдоль каждого горизонтального участка равна нулю, а вдоль каждого вертикального — произведению —mg на длину этого участка. Но суммарная длина всех вертикальных отрезков от точки α до точки b всегда равна h, поэтому полная работа на пути любой формы равна —mgh. Если сила не постоянна по величине и направлению, ее следует разложить на вертикальную и горизонтальную составляющие на каждом отрезке ломаной кривой, после чего, правильно сложив все элементарные работы, мы получим тот же результат.
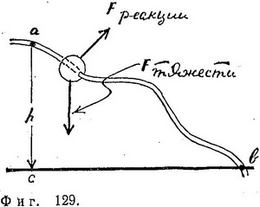
В качестве хорошей иллюстрации могущества этой теоремы рассмотрим движение бусинки, соскальзывающей без трения вдоль проволоки произвольной формы, как показано на фиг. 129. Исследование такого рода задач привело физиков восемнадцатого века к введению понятия энергии. По определению, движение без трения обозначает, что проволока не оказывает на бусинку никакого воздействия вдоль направления ее движения. Сила, с которой проволока действует на бусинку, перпендикулярна направлению движения — эта сила вынуждает бусинку оставаться на проволоке. Однако сила, которая все время перпендикулярна направлению движения, не совершает никакой работы1. Работу совершает лишь гравитационная сила, всегда направленная вниз. Однако направление движения частицы непрерывно изменяется, так что для вычисления работы гравитационной силы необходимо разбить действительный путь на маленькие отрезки, спроектировать силу на направление движения на каждом отрезке и сложить все элементарные работы. Если путь сложен, задача нахождения работы тоже сложна. При этом, если мы хотим узнать все подробности движения, эту сложную задачу следует решать с использованием второго закона Ньютона.
Предположим, однако, что нас интересует лишь скорость частицы в точке b, если она вначале покоилась, скажем, в точке α. Если использовать полученный выше результат, то вычисления в этом случае займут лишь несколько строк. Из теоремы 11.3 следует, что:
Тb—Тα — работе, совершенной над бусинкой при перемещении ее из α в b. (12.11)
1) Это можно описать другими словами: «Представим ситуацию, когда частица вынуждена перемещаться вдоль сложного пути под действием сил, не совершающих никакой работы, т. е, сил, всегда перпендикулярных направлению движения?»
В точке α бусинка покоилась, так что vα = 0 и Тα = 0. Поэтому:
Следовательно, скорость в точке b:
Мы привели эти вычисления так подробно, чтобы подчеркнуть один замечательный факт. Всё, что нам потребовалось для вычисления конечной скорости, была работа, совершенная над частицей. Чтобы найти эту работу непосредственно вдоль искривленного пути, соответствующего форме проволоки, необходимо было решать очень сложную задачу, чего мы постарались избежать. Мы воспользовались тем, что работа, произведенная над частицей при перемещении ее из α в b, не зависит от пути, и вычислили ее, выбрав наиболее простой путь — из α в c вертикально вниз, где работа, совершенная на длине h, равна mgh, а затем из c в b по горизонтальному пути, где работа равна нулю, так как сила перпендикулярна направлению движения,
В этом суть достигнутого нами упрощения. Если силы консервативные, то для вычисления их работы над частицей, которая перемещается из одной точки в другую, нет необходимости следовать вдоль действительной траектории частицы, а можно выбирать любой путь. Избрав самый простой из них, мы легко находим величину работы.