Решения уравнения Шредингера, а, следовательно, и уровни энергии для электрона, находящегося под действием кулоновской силы, приложенной к нему со стороны протона (атом водорода), характеризуются тремя квантовыми числами:

n, l, m_l

где l и m_l — азимутальные квантовые числа, а n — главное квантовое число, определяющее стоячую волну де Бройля, которая описывает радиальную зависимость волновой функции электрона, находящегося в поле кулоновской силы. Эти три квантовых числа (их три, так как задача трехмерная) не являются независимыми, как было в случае частицы, заключенной в кубическом сосуде (числа n_x, n_y и n_z могли принимать любые целые значения), а связаны друг с другом следующим образом.

Главное квантовое число n может принимать любые целые положительные значения:

n = 1, 2, 3, 4….

Квантовое число, характеризующее полный угловой момент, может принимать любые целые значения меньше n:

l = n—1, n—2, …,0,

а магнитное квантовое число m_l (как уже было сказано) — следующие значения:

m_l = l, l—1, …,—l.

Энергетические уровни определяются только главным квантовым числом и в точности совпадают с уровнями, полученными Бором:

На фиг. 155 изображена диаграмма энергетических уровней атома водорода, полученная на основании решения уравнения Шредингера.

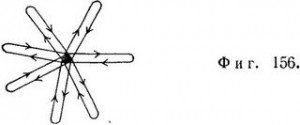
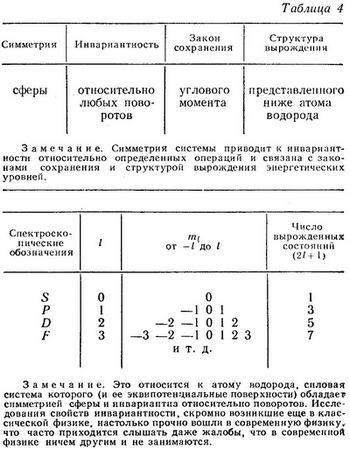
S-состояния, или состояния с нулевым угловым моментом (табл. 4), более или менее сферически симметричны. Их можно сравнить с классическим движением, направленным к центру или от центра и изображенным на фиг. 156. Угловые моменты Р-, D-,… состояний соответственно равны 1, 2, …. При заданном значении п состояние с максимальным возможным угловым моментом (l = n—1) соответствует вращению электрона по круговой орбите.

Уровни энергии других атомов, начиная с гелия и далее, несколько отличаются, как мы увидим, от энергетических уровней атома водорода; в общем случае структура уровней произвольного атома сходна со структурой уровней водородного атома, только расстояния между уровнями будут иными.

Далее, когда мы говорим о коллективе невозмущенных атомов, заключенных в охлажденном сосуде или движущихся в пространстве, мы имеем в виду, что каждый из таких атомов находится в основном состоянии. Следовательно, наборы одинаковых атомов являются тождественными физическими системами. Этим объясняется известный факт, что два атома водорода или два атома гелия ничем не отличаются друг от друга. Это невозможно истолковать с классической точки зрения; так, если рассмотреть, например, солнечную систему, то ниоткуда не будет следовать, что орбита одной планеты должна совпадать с орбитой другой или что две солнечные системы обязаны быть тождественными, даже если законы движения и силы, действующие между солнцами и планетами, будут абсолютно одинаковыми. В классическом случае дискретные состояния не существуют, поэтому, насколько нам известно, солнечные системы, в отличие от атомов, должны различаться между собой.