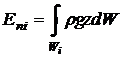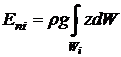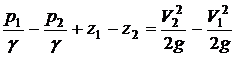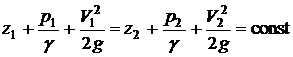Рассмотрим установившееся течение жидкости, находящейся под воздействием только одной массовой силы — веса жидкости. Выделим в потоке струйку, такую малую, что изменением параметров в ее поперечном сечении можно пренебречь и считать их постоянными. За бесконечно малый промежуток времени Dt участок струйки 1— 2 переместится в положение 1?— 2?.

Применим к этой струйке уравнение энергии, заключающееся в том, что работа сил по перемещению струйки равна приросту кинетической энергии этой струйки.

Известно, что элементарная работа силы определяется выражением:

Работа поверхностных сил давления тогда составит:

Т. к. в первом сечении направление сил давления совпадает с направлением вектора скорости, а во втором сечении оно противоположно, то:

Заметим, что работа сил давления, действующих по боковым поверхностям струйки равна 0, вследствие ортогональности векторов давления и скорости. Суммарная работа поверхностных сил определится выражением:

Элементарная работа массовых сил (сил веса) определяется изменением потенциальной энергии выделенного элемента массы:

Потенциальная энергия массы, заключенной в объеме W определяется выражением:

Учитывая, что для несжимаемой жидкости r= const, получим:

Объем, занимаемый струйкой в начальном и конечном положениях можно представить в виде двух составляющих, рис. 3.1.

Масса жидкости, заключенная в объемах W1 и W2 определится как:

Т. к. приток массы в рассматриваемой струйке отсутствует, то:

M1 = M2

следовательно:

W1 = W2

Нетрудно заметить, что объем 1?-2 для рассматриваемых положений является общим, тогда:

или

Это выражение определяет закон сохранения массы для струйки несжимаемой жидкости. С учетом отмеченного:

где dG = rgdW — элементарный вес жидкости, заключенный в объеме dW. 

Т. е.

Применяя такой же прием, получим выражение для прироста кинетической энергии струйки:

Запишем уравнение баланса энергии:

Подставляя имеющиеся выражения в данную формулу, получим:

после преобразований, с учетом того, что dW1 = dW2 =dW =dG/g, получаем:

или, после перегруппирования членов:

Это выражение и представляет собой уравнение Бернулли для идеальной несжимаемой жидкости.
Величина  называется скоростным напором, 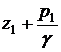 определена ранее как гидростатический напор, а величина  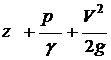получила название полный напор.

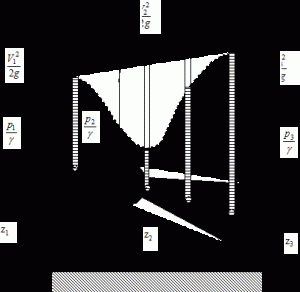
Рис. 3.2

Таким образом, согласно уравнению Бернулли, полный напор представляет собой сумму гидростатического и скоростного напора и для выделенной струйки жидкости это величина постоянная. Проиллюстрируем это положение графиком, см. рис. 3.2.