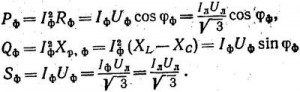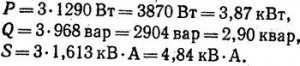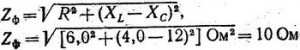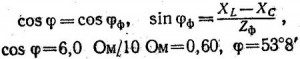Пример

В каждую фазу трехфазной четырехпроводной цепи нейтральным проводом включены сопротивления, как показано на рис. 61, а (соединение звездой). Сопротивления во всех фазах одинаковы и равны: активные 8,0 Ом, индуктивные 12 Ом, емкостные 6,0 Ом. Линейное напряжение сети 220 В. Для каждой фазы нагруз­ки определить: 1) полное сопротивление, коэффициент мощности, сдвиг фаз между током и напряжением, фазные токи; активную, ре­активную и полную мощности каждой фазы; 2) линейные токи, ток в нейтральном проводе; активную, реактивную и полную мощности потребителя. Построить векторную диаграмму.

Дано: r₁=r₂= r₃=Rф=8,0 Ом — активные сопротивления фаз; X_L1=X_L2=X_L3=X_Lф =12 Ом — индуктивные сопротивления фаз; X_C1=X_C2=X_C3=X_Cф=6,0 Ом — емкостные сопротивления фаз; U_л=220 В — линейное напряжение.

Найти: 1) Z_ф— полное сопротивление каждой фазы; cos φ_ф— коэффициент мощности; φ_ф— сдвиг фаз между током и напряжени­ем; I_ф—фазные токи; Р_ф, Q_ф, S_ф  — соответственно активную, ре­активную, полную мощности; 2) I_л — линейные токи, I₀— ток в нейтральном проводе; P,Q,S— активную, реактивную, полную мощности нагрузки.

Решение. 1) Так как в данной задаче соответствующие со­противления всех фаз одинаковы (симметричная нагрузка), доста­точно произвести вычисления для одной фазы. Полное сопротивле­ние фазы найдем по формуле:

Вычисляем полное сопротивление фазы:

Коэффициент мощности фазы определим по формуле:

затем найдем сдвиг фазы φ_ф между током и напряжением. Для опре­деления направления сдвига фаз определим sin φ_ф:

Если sin φ_ф>0 (нагрузка преимущественно индуктивная), ток от­стает от напряжения на угол φ_ф; если sin φ_ф<0 (нагрузка преиму­щественно емкостная), ток опережает напряжение по фазе.

Находим коэффициент мощности фазы:

так как sin φ_ф >0, то ток отстает по фазе от напряжения, и на век­торной диаграмме вектор тока сдвинут на 36°52′ в сторону отстава­ния (по часовой стрелке) от вектора напряжения. При симметрич­ной нагрузке коэффициент мощности всей нагрузки равен коэффи­циенту мощности фазы: cosφ=cos φ_ф=0,80.

Фазные токи найдем по закону Ома:

При соединении звездой с нейтральным проводом напряжение на каждой фазе, независимо от вида и сопротивления фазы, всегда оди­наково и равно U_ф =U_л /√(3), тогда I_ф = U_л/√(3)Z_ф. При соедине­нии звездой линейные токи равны фазным:

Находим фазные и линейные токи:

Активную, реактивную и полную мощности фаз определяем из формул:

Подставляя числовые значения, находим активную, реактивную и полную мощности фазы:

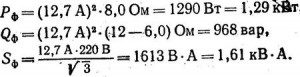
2) Ток в нейтральном проводе определяется по векторной диаг­рамме:

При симметричной нагрузке ток в нейтральном проводе I₀=0.

Активная мощность всей нагрузки равна сумме активных мощ­ностей фаз:

Для симметричной нагрузки Р = ЗР_ф =√(3), I_л U_л cos φ_ф

Реактивная мощность нагрузки равна алгебраической сумме реактивных мощностей фаз:

(Знак «+» при преобладании индуктивной нагрузки, «—» — ем­костной.) В данной задаче:

Определим полную мощность нагрузки как:

В данной задаче S=3S_ф

Находим активную, реактивную и полную мощности нагрузки:

Строим векторную диаграмму (см. рис. 61, б). Построение начинаем с фазных напряжений, располагая их под углом  120°  друг к другу. Под углами φ_А, φ_Б, φ_С (в данной задаче 36°52′) к соответ­ствующим векторам фазных напряжений строим векторы фазных токов; I_ф=12,7 А, U_ф=127 В.

Ответ. 1) Полное сопротивление фазы 10 Ом; коэффициент мощности 0,80; сдвиг фаз между током и напряжением 36°52′; фазные и линейные токи 12,7 А; мощности фазы: активная 1,29 кВт, реактивная 0,968 вар, полная 1,61 кВ*А; 2) ток в нейтральном про­воде равен нулю; мощность нагрузки: активная 3,87 кВт, реак­тивная 2,90 квар, полная 4,84 кВ*А.

Пример

Потребитель, представляющий собой симметричную нагрузку, фазы которой соединены треугольником, включен в сеть трехфазного тока с линейным напряжением 220 В (рис. 62). Соот­ветствующие сопротивления во всех фазах одинаковы и равны: ак­тивные 6,0 Ом, индуктивные 4,0 Ом, емкостные 12 Ом. Определить: полное сопротивление каждой фазы, коэффициент мощности фазы, фазные и линейные токи; активную, реактивную, полную фазные мощности; активную, реактивную и полную мощности нагрузки.

Дано: U_л—220 В — линейное напряжение цепи; r₁=r₂=r₃ =R=6,0 Ом — активные сопротивления фаз; X_L1=X_L2=X_L3=X_L= 4,0 Ом — индуктивные сопротивления X_C1=X_C2=X_C3=X_C = 12 Ом — емкостные сопро­тивления фаз.

Найти: Z_ф— полное сопротивление каждой фазы, cos φ_ф— коэффициент мощности фазы, I_ф, I_л — фазные и линиейные токи; ; Р_ф, Q_ф , S_ф — активную, реактивную, полную мощности фаз; Р,Q, S — активную, реактивную и пол­ную мощности нагрузки.

Решение. При симметричной на­грузке достаточно определить все необ­ходимые величины для одной фазы.

Полное сопротивление фазы найдём по формуле:

Коэффициент мощности фазы:

в данной задаче коэффициент мощности всей нагрузки:

Фазный ток находим по закону Ома для участка цепи:

При соединении треугольником фазное напряжение равно линейному, U_ф =U_л, поэтому I_Ф=U_л/Z_ф.

Для нахождения линейного тока учитываем, что при симметрич­ной нагрузке:

Подставляя числовые значения, получаем: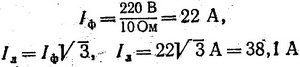

Соответствующие мощности фаз определяем по формулам:

Активную мощность нагрузки определим по формуле:

Находим реактивную мощность нагрузки:

Определяем полную мощность нагрузки:

Ответ. Полное сопротивление фазы 10 Ом, коэффициент мощ­ности фазы 0,60, фазные токи 22 А, линейные токи 38,1 А; мощ­ности фаз: активная 2,9 кВт, реактивная 3,87 квар, полная 4,84 кВ*А; мощности нагрузки: активная 8,7 кВт, реактивная —11,6 квар; полная 14,5 кв*А.