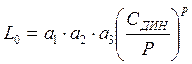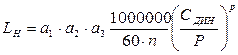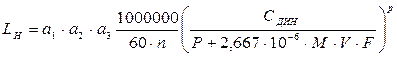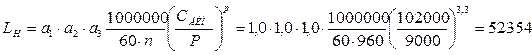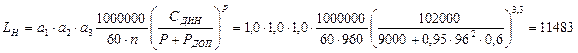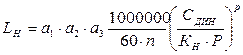Расчет долговечности подшипника традиционно проводится по модифицированному уравнению долговечности, принятому организацией ИСО:
где L0 – номинальная долговечность в миллионах оборотов; a1 – поправочный коэффициент надежности; a2 – поправочный коэффициент материала; a3 — поправочный коэффициент условий работы; CДИН – динамическая грузоподъемность подшипника; P – эквивалентная нагрузка на подшипник; р — показатель степени.
Если подшипник работает в длительном режиме, вращается с постоянной скоростью, появляется возможность рассчитать срок службы в часах:
где LH – срок службы подшипника в часах, n – частота вращения вала мин-1.
В работе предложено оценивать влияние вибрации на срок службы подшипников по следующей формуле:
где M – вес противонаправленной вибрации кгс; V – виброскорость, мм/с; F – частота вибрации, циклы/мин.
Предварительный анализ формулы указывает на несовпадение размерностей в знаменателе. Очевидно, M – масса противонаправленной вибрации, кг. Неопределенность термина «противонаправленная вибрация» не позволяет определить способ получения значений этой величины. Обратимся, к примеру, приведенному в работе.
Пример.
Статическая нагрузка – 400 кГС, частота вращения – 1800 мин-1, динамическая грузоподъемность – 8000 кГС, масса — 5200 кг. Предполагается, что коэффициенты a1, a2, a3– равны 1,0. Результаты расчета приведены в таблице 1. Воссоздать последовательность расчета, несмотря на использование единиц кгс не сложно. Результаты несколько отличаются, приведены в скобках.
Таблица 1 – Результаты расчета срока службы подшипника с учетом вибрации
| Виброскорость, мм/с | Нагрузка на подшипник, кгс | Срок службы | % срока службы, в сравнении с 5 мм/с |
| 8,46 лет (7408 часов) | 228,0 | ||
| 3,7 лет (3276 часов) | 100,0 | ||
| 1,94 лет (1729 часов) | 52,0 | ||
| 1,115 лет (1020 часов) | 31,0 | ||
| 5,6 мес. (457 часов) | 13,0 | ||
| 37,5 | 1350 (1336) | 2,5 мес. (198 часов) | 6,0 |
| 1667 (1648) | 1,4 мес. (106 часов) | 3,0 | |
| 2,3 нед. | 1,1 |
Трудно объяснить столь завышенные результаты расчетов. Существуют несколько факторов не позволяющих рекомендовать данную формулу.
- Возможно, данная формула имеет эмпирический характер и адекватна лишь для узкого круга машин.
- Термин «вес противонаправленной вибрации» является неопределенным и не позволяет определить способ нахождения значений величины.
- Расчеты следует выполнять в системе СИ в XXI веке.
- Значение коэффициента 2,667∙10-6 вряд ли возможно использовать для иных механизмов.
- Вибрация механизма имеющего массу 5200 кг при значениях 25 мм/с и более, возможна в течение короткого промежутка времени, исчисляемого в лучшем случае в сутках, если не в часах до разрушения элементов.
Следует найти способ расчета долговечности подшипников, учитывающий индивидуальные особенности механизма и применимого как на этапе проектирования, так и на этапе эксплуатации. Часто после балансировки уровень вибрации опор снижается в 10…12 раз. Увеличение срока службы подшипников, можно рассчитать исходя из снижения нагрузки на подшипниковые узлы по значению уравновешенной центробежной силы:
РДОП = mK∙ω2∙rК,
где mK — масса компенсирующего груза, кг; ω – угловая скорость ротора, рад/с; rК — радиус установки компенсирующего груза, м.
Для снижения вибрации от 16,2 мм/с до 3,8 мм/с на рабочее колесо (массой 900 кг) вентилятора ДН-13 был установлен компенсирующий груз массой 0,95 кг на радиусе 0,6 м. Установленные подшипники 3516 имеют динамическую грузоподъемность 102 кН. Частота вращения 960 мин-1. При консольном расположении рабочего органа (рабочего колеса) практически вся нагрузка приходится на подшипник ближайший к ротору. Расчетная долговечность составит:
Это составляет почти 6 лет непрерывной работы. Рассчитаем снижение срока службы подшипника при постоянной вибрации 16,2 мм/с:
или 1,3 года непрерывной работы. Практически замена подшипников на данной установке осуществлялась ежегодно.
Отношение известного уравновешенного дисбаланса D = mK∙rК = 0,95∙0,6 = 0,57 кг∙м к значению снижения виброскорости V мм/с (в рассматриваемом случае 16,2 – 3,8 = 12,4 мм/с) позволяет определить коэффициент балансировочной чувствительности:
КБЧ = D/V = 0,57/12,4 = 0,046 кг∙м/(мм/с).
Тогда, формула для расчета примет следующий вид:
Дополнительным фактором, приводящим к снижению ресурса подшипника, является воздействие осевой вибрации, возникающей при дисбалансе ротора. Причина осевой вибрации – изгиб вала под воздействием неуравновешенной центробежной силы. Воздействие осевой нагрузки в расчете долговечности подшипника качения учитывается при определении эквивалентной динамической нагрузки на подшипник [6]:
P = X∙Ft + Y∙Fa,
где P – эквивалентная динамическая нагрузка на подшипник, Н; Ft – фактическая радиальная нагрузка на подшипник, Н; Fa – фактическая осевая нагрузка на подшипник, Н; X – коэффициент радиальной нагрузки на подшипник, Y – коэффициент осевой нагрузки на подшипник.
Если определение значения радиальной нагрузки часто не представляет затруднений, то оценить значения осевой нагрузки при эксплуатации — сложная задача. Решение возможно в случае рассмотрения следов износа подшипника. Многое определяет тип рассматриваемого подшипника. Однако, основной причиной осевой нагрузки является изгиб вала.
Изгиб вала возникает: при воздействии сил гравитации, при воздействии вибраций передающихся на неработающее оборудование, при одностороннем тепловом воздействии, при воздействии неуравновешенных сил, при одностороннем нагружении, при ошибках монтажа, при несоосности валов, при износе посадочных мест и по иным причинам. Данный дефект – весьма характерен не только для длинных, но и для коротких валов.
Роликовые подшипники весьма чувствительны к перекосам. Поэтому изгиб вала приводит к неравномерному распределению нагрузки по длине ролика, и как следствие к неравномерному износу роликов (рисунок 1).
Рисунок 1 – Неравномерный износ роликов при изгибе вала
Двухрядный шарикоподшипник способен компенсировать перекосы до 2030′. Следы износа не только позволят определить угол перекоса, но и оценить неравномерность распределения нагрузки по беговым дорожкам подшипника (рисунок 2). Степень неравномерности определится отношением длин участков осповидного выкрашивания по дорожкам.
Рисунок 2 – Неравномерное осповидное выкрашивание по беговым дорожкам двухрядного шарикового подшипника
Воздействие осевой нагрузки может привести к тому, что в работе окажется лишь один ряд роликов (рисунок 3). Это результат осевого смещения вала в результате ошибки монтажа. Такой режим работы, очевидно должен привести к снижению динамической грузоподъемности подшипника.
Рисунок 3 – Следы воздействия осевого смещения вала на наружном кольце двухрядного роликового подшипника
Снижение долговечности при неравномерном распределении нагрузки в подшипнике в продольном направлении относительно вала предлагается учитывать при помощи коэффициента КН = 1,0…2,0:
Максимальное снижение долговечности при работе одной беговой дорожки в двухрядном роликоподшипнике (при КН = 2,0) и составит 23,3 = 9,8 раз. Для роликового подшипника коэффициент определяется отношением всей длины ролика к длине изношенной части.
Отсутствие тепловых зазоров приводит к возникновению значительных сил определяемых площадью сечения вала:
Fa = E∙S∙α∙Δt,
где E – модуль Юнга, МПа; S – площадь сечения вала, м2; α — коэффициент линейного расширения, 1/град.; Δt – повышение температуры, 0С.
Если на валу механизма установлены шариковые подшипники, возникшая осевая сила проявится в виде смещения следов контакта тел качения с беговой дорожкой (рисунок 4).
Рисунок 4 – Смещение следов контакта тел качения и беговой дорожки в шарикоподшипнике при воздействии осевой силы
Данное смещение тел качения приводит к исчезновению радиального зазора и возникновению значительных радиальных сил определяемых геометрией подшипника. Значение радиальной составляющей:
Ft = Fa∙tgφ,
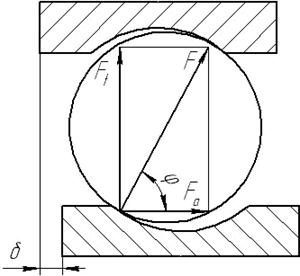
где φ – угол между силами F и Fa (рисунок 5); F – результирующая реакция, направленная перпендикулярно к контактирующей поверхности. Угол φ определяется допустимой осевой игрой δ и диаметром тел качения dW:
φ = arccos(δ/dW).
Рисунок 5 – Схема распределения сил в подшипнике качения при отсутствии радиального зазора
Так как угол φ близок к 900 радиальные силы могут увеличиться до такой степени, что это приведет к разрушению наружного кольца (рисунок 6).
Рисунок 6 – Разрушение наружного кольца шарикоподшипника при отсутствии теплового зазора
Вал диаметром 40 мм при нагреве на 20 0С при отсутствии возможного теплового расширения создает осевую силу:
Fa = E∙S∙α∙Δt = 2∙105∙π∙202∙12∙10-6∙20 = 60288 Н.
Установленный на валу подшипник 307 (допустимая осевая игра δ = 0,02 мм, диаметр тел качения dW = 14,3 мм) испытывает следующую радиальную нагрузку:
φ = arccos(δ/dW) = arccos(0,02/14,3) = 89,9 град,
Ft = Fa∙tgφ = 60288∙tg89,90 = 34542444 Н.
Статическая грузоподъемность данного подшипника С = 26200 Н.