Введем теперь одно очень полезное представление. Допустим, что тело занимает определенное положение в пространстве. Каким образом можно зафиксировать это положение? Часто мы отмечаем положение тела, исходя из положения другого объекта; например, мы говорим: «две мили от Таймс-сквер» или «полмили от Эйфелевой башни, если идти в направлении Сены». Нас мало интересует абсолютное положение предмета. Положим, ваш друг сломал ногу в Альпах. В то время Земля находилась в определенной точке своей орбиты, Солнце — в какой-то точке своего пути через Галактику и т. д. Тем не менее врача не интересовали все эти подробности. Его интересовал лишь тот факт, что перелом произошел в пяти сантиметрах выше лодыжки в кости, называемой большой берцовой. Одно из свойств нашего мира проявилось здесь н том, что ваш друг может перемещаться вместе со своим переломом, причем положение последнего относительно лодыжки и колена будет оставаться неизменным. В данном случае в качестве удобной системы отсчета может служить нога человека. Тогда перелом будет расположен в пяти сантиметрах над лодыжкой.
Остров Манхэттен в Нью-Йорке является очень удобной территорией для определения местоположения, поскольку большинство его улиц образует прямоугольную сетку. Даже незнакомый с городом человек легко найдет место, которое ему указали как «угол 6-й авеню и 42-й стрит». Конечно, это указывает не область в абсолютном пространстве, а некое место относительно других улиц и зданий Манхэттена, а, следовательно, поскольку Земля жесткая, — относительно других мест па Земле. Наше пространство трехмерно; однако, поскольку наши действия обычно ограничены земной поверхностью, для нас указание «угол 6-й авеню и 42-й стрит» является вполне достаточным. При этом подразумевается, что встреча состоится на улице. Последнее, конечно, не обязательно. Она может состояться и на четвертом этаже здания, расположенного на углу 6-й авеню и 42-й стрит.
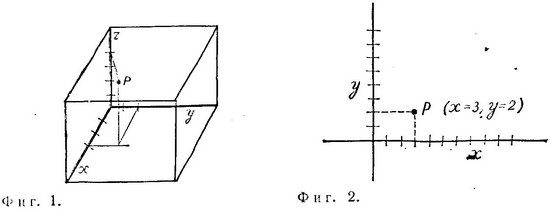
Эта исключительно простая идея1) формально обобщается с помощью понятия системы координат. Три пространственных измерения представляются в виде взаимно перпендикулярных осей х, у и z (фиг. 1). Положение точки определяется тогда, например, так: «три единицы вдоль х, две — вдоль у и четыре — вдоль z» либо набором из трех чисел, соответствующих значениям х, у и z [так, (3, 2, 4) означает, что х=3, у=2, 2=4]. Это все равно что сказать: «6-я авеню вдоль х, 42-я стрит вдоль у и 4-й этаж вдоль z».
Часто изображают лишь два измерения, поскольку во многих задачах то, что можно показать для трех измерений, легко демонстрируется для двух. Типичная двумерная система координат изображена на фиг. 2. Две взаимно перпендикулярные оси характеризуют положение точек на плоскости. Точка, отмеченная на фиг. 2, имеет координаты х=3 и у=2. Если кто-нибудь скажет: «Встретимся в точке х=3 и у=2», то такое утверждение будет иметь однозначный смысл, если второй человек знает, что оно относится к данной системе координат.
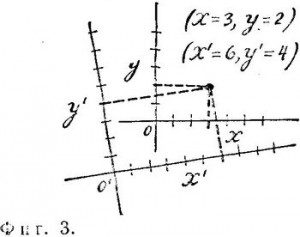
Далее, абсолютно очевидно, что та же самая точка будет иметь другие номера авеню и стрит, если Фиг. 3. Рассматривать ее относительно улиц другого города или в другой координатной системе (фиг. 3). В новой системе, оси которой (или авеню и стриты) обозначены через х’ и у’, эта точка имеет координаты х’=6 и у’=4. Координаты физической точки Р зависят от той сетки, относительно которой эта точка рассматривается.
1) Впервые эта идея была выдвинута Декартом в его объединении алгебры и геометрии (аналитической геометрии). С каждой точкой трехмерного пространства ему удалось связать три числа (x, y, z), ас каждой тройкой чисел — точку в пространстве. Тогда все геометрические объекты и теоремы представляются как алгебраические объекты и алгебраические соотношения.
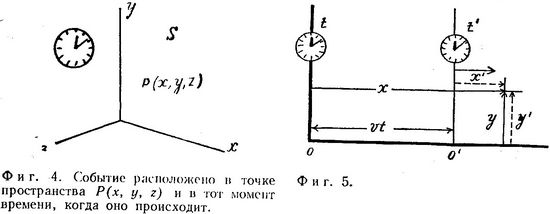
Иногда желательно зафиксировать так начинаемое событие, или точку в пространстве и времени. Для этого надо иметь три пространственных и временное намерения (фиг. 4).
Вскоре нам потребуются координатные системы, равномерно движущиеся друг относительно друга (для удобства системы координат будут называться либо «неподвижными», либо «движущимися»). Представим, что в момент t=0 осп х и у двух координатных систем совпадали, а движение происходит вдоль оси х (фиг. 5). Через временной интервал t начало «движущейся системы координат» О’ будет находиться на расстоянии vt от начала «неподвижной системы» О. Таким образом, событие, происходящее в пространственно-временной точке Р, имеет координаты (х, у, t) в «неподвижной системе отсчета» и координаты (х’, у’, t’) в «движущейся системе», причем в соответствии с обычными правилами:
x` = x – vt,
y` = y,
t` = t.