Для получения полной информации о положении точки на физической поверхности Земли используется третья координата – высота.

За начало отсчета высот принимается средний уровень Балтийского моря, являющегося основной уровнённой поверхностью, совпадающей с поверхностью геоида. Положение среднего уровня Балтийского моря определено в результате многолетних наблюдений и отмечено на футштоке на водомерном посту в г. Кронштадте.

Футшток – рейка с делениями, укрепленная отвесно на берегу так, чтобы обеспечивалась возможность отсчитывания по ней положения поверхности воды, находящейся в спокойном состоянии. Кронштадтский футшток – черта на медной пластине, вмонтированной в гранитный устой Синего моста Обводного канала в г. Кронштадте. Первый футшток был установлен во времена правления Петра I, и в 1703 г. начались регулярные наблюдения за уровнем Балтийского моря. Вскоре футшток был разрушен и только с 1825 г. (и до настоящего времени) были возобновлены регулярные наблюдения. В 1840 г. гидрографом М.Ф.Рейнеке была вычислена высота уровня Балтийского моря и зафиксирована на гранитном устое моста в виде глубокой горизонтальной черты. С 1872 г. эта черта принята за нулевую отметку при вычислении высот всех точек на территории государства. Кронштадский футшток неоднократно видоизменялся, однако положение его основной отметки при изменениях конструкции сохраняли прежней, т.е. определенной в 1840 г.

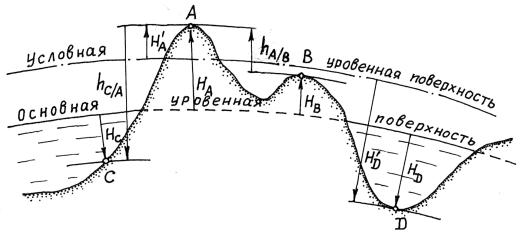
Положение точки определяется расстоянием от нее по линии направления силы тяжести до основной уровенной поверхности (рис. 2.14). Это расстояние называют абсолютной высотой точки.

Рис. 2.14. Система высот.

Абсолютные высоты H могут быть положительными (для точек, находящихся в нашем представлении выше уровня Балтийского моря), и отрицательными – для точек, находящихся ниже уровня Балтийского моря. Например, абсолютные высоты точек А и В – положительные, а абсолютная высота точки С – отрицательная.

Разность абсолютных высот двух точек называется относительной высотой или превышением, обозначаемым буквой h:

h = HA − HB. (2.14)

Превышение одной точки над другой также может быть положительным и отрицательным. Если абсолютная высота точки А больше абсолютной высоты точки В, т.е. находится выше точки В, то превышение точки А над точкой В будет положительным, и наоборот, превышение точки В над точкой А – отрицательным.

Пример 2.6. Абсолютные высоты точек А и В : НА = +124,78 м; НВ = +87,45 м. Найти взаимные превышения точек А и В.

Решение.

Превышение точки А над точкой В hА(В) = +124,78 – (+87,45) = +37,33 м. Превышение точки В над точкой А hВ(А) = +87,45 – (+124,78) = — 37,33 м.

Пример 2.7. Абсолютная высота точки А равна +124,78 м. Превышение точки С над точкой А равно hC(А) = — 165,06 м.

Найти абсолютную высоту точки С.

Решение.

По формуле (2.14) абсолютная высота точки С равна НС = НА + hC(А) = +124,78 + +(- 165,06) = — 40,28 м.