В данном случае двоичный код первичного алфавита строится цепочками равной длины, т.е. со всеми знаками связано однообразное количество инфы равное I(А) = log2 N. Сформировывать признак конца знака не требуется, потому для определения длины кода можно пользоваться формулой К(А,2) > log2 N. Приемное устройство просто отсчитывает обсужденное заблаговременно количество простых сигналов и интерпретирует цепочку (устанавливает, какому знаку она соответствует), соотнося ее с таблицей кодов. Правда, при всем этом недопустимы сбои, к примеру, пропуск (непрочтение) 1-го простого сигнала приведет к сдвигу всей кодовой последовательности и неверной ее интерпретации; решается неувязка методом синхронизации передачи либо другими методами, о которых речь пойдет в гл. 5. С другой стороны, применение равномерного кода оказывается одним из средств контроля корректности передачи, так как факт поступления излишнего простого сигнала либо, напротив, поступление неполного кода сходу интерпретируется как ошибка.
Примером равномерного алфавитного кодировки является телеграфный код Бодо, пришедший на замену азбуке Морзе. Начальный алфавит должен содержать менее 32-х знаков; тогда К(А,2) = log2 32 = 5, т.е. каждый символ первичного алфавита содержит 5 бит инфы и кодируется цепочкой из 5 двоичных символов. Условие N ≤ 32, разумеется, производится для языков, основанных на латинском алфавите (Т = 27 = 26 + «пробел»), но в российском алфавите 34 буковкы (с пробелом) — конкретно по этой причине пришлось «сжать» алфавит (как в коде Хаффмана) и соединить в один символ «е» и «ё», также «ь» и «ъ», что видно из табл. 3.1. После такового сжатия N = 32, но, не остается свободных кодов для символов препинания, потому в телеграммах они отсутствуют либо заменяются буквенными аббревиатурами; это не является приметным ограничением, так как, как указывалось выше, избыточность языка позволяет просто вернуть информационное содержание сообщения. Избыточность кода Бодо для российского языка Q(r,2) = 0,148, для британского Q(e,2) = 0,239.
Другим принципиальным для нас примером использования равномерного алфавитного кодировки является представление символьной (знаковой) инфы в компьютере. Чтоб найти длину кода, нужно начать с установления количество символов в первичном алфавите. Компьютерный алфавит должен включать:
- 26 х 2 = 52 букв латинского алфавита (с учетом строчных и строчных);
- 33 х 2 = 66 букв российского алфавита;
- числа 0.. .9 — всего 10;
- знаки математических операций, знаки препинания, спецсимволы ≈ 20.
Получаем, что общее число знаков N ≈ 148. Сейчас можно оценить длину кодовой цепочки: К(с,2) ≥ log2148 ≥ 7,21. Так как длина кода выражается целым числом, разумеется, К(с,2) = 8. Конкретно таковой метод кодировки принят в компьютерных системах: хоть какому символу ставится в соответствие код из 8 двоичных разрядов (8 бит). Эта последовательность сохраняется и обрабатывается как единое целое (т.е. отсутствует доступ к отдельному биту) — по этой причине разрядность устройств компьютера, созданных для хранения либо обработки инфы, кратна 8. Совокупа восьми связанных бит получила заглавие б, а представление таким образом знаков — байтовым кодировкой.
Б вместе с битом может употребляться как единица измерения количества инфы в сообщении. Один б соответствует количеству инфы в одном знаке алфавита при их равновероятном рассредотачивании. Этот метод измерения количества инфы именуется также большим. Пусть имеется некое сообщение (последовательность символов); оценка количества содержащейся в нем инфы согласно рассмотренному ранее вероятностному подходу (при помощи формулы Шеннона (2.17)) дает Iвер, а большая мера пусть равна Iоб; соотношение меж этими величинами вытекает из (2.7):
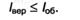
Конкретно б принят в качестве единицы измерения количества инфы в интернациональной системе единиц СИ. 1 б = 8 бит. Вместе с б для измерения количества инфы употребляются более большие производные единицы:

Внедрение 8-битных цепочек позволяет закодировать 28=256 знаков, что превосходит оцененное выше N и, как следует, дает возможность употребить оставшуюся часть кодовой таблицы для представления дополнительных знаков.
Но недостаточно только договориться об определенной длине кода. Ясно, что методов кодировки, т.е. вариантов сравнения знакам первичного алфавита восьмибитных цепочек, сильно много. По этой причине для сопоставимости технических устройств и обеспечения способности обмена информацией меж многими потребителями требуется согласование кодов. Схожее согласование осуществляется в форме стандартизации кодовых таблиц.
Первым таким интернациональным эталоном, который применялся на огромных вычислительных машинах, был EBCDIC (Extended Binary Coded Decimal Interchange Code) — «расширенная двоичная шифровка десятичного кода обмена». В компьютерах и телекоммуникационных системах применяется интернациональный байтовый код ASCII (American Standard Code for Information Interchange — «американский стандартный код обмена информацией»).
Он регламентирует коды первой половины кодовой таблицы (номера кодов от 0 до 127, т.е. 1-ый бит всех кодов 0). В эту часть попадают коды строчных и строчных британских букв, числа, знаки препинания и математических операций, также некие управляющие коды (номера от 0 до 31), вырабатываемые при использовании клавиатуры. Ниже приведены некие ФSC-коды:
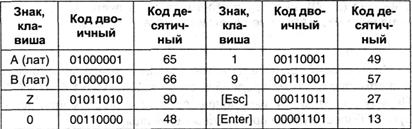
2-ая часть кодовой таблицы — она считается расширением основной — обхватывает коды в интервале от 128 до 255 (1-ый бит всех кодов 1). Она употребляется для представления знаков государственных алфавитов (к примеру, российского), также знаков псевдографики. Для этой части также имеются эталоны, к примеру, для знаков российского языка это КОИ-8, КОИ-7 и др.
Как в основной таблице, так и в ее расширении коды букв и цифр соответствуют их словарному порядку (т.е. порядку следования в алфавите) — это обеспечивает возможность автоматизации обработки текстов и ускоряет ее.
В текущее время появился и находит все более обширное применение очередной интернациональный эталон шифровки — Unicode. Его особенность в том, что в нем применено 16-битное кодирование, т.е. для представления каждого знака отводится 2 б. Такая длина кода обеспечивает включения в первичный алфавит 65536 символов. Это, в свою очередь, позволяет сделать и использовать единую для всех всераспространенных алфавитов кодовую таблицу.