Рассмотренные нами простые механизмы применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Естественно возникает вопрос: давая выигрыш в силе или в пути, не дают ли простые механизмы выигрыша и в работе? Ответ на поставленный вопрос можно получить из опыта.
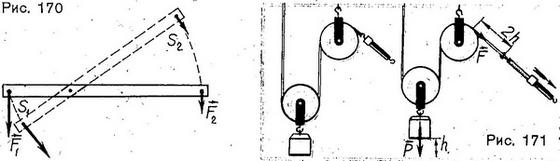
Уравновесив на рычаге две какие-нибудь разные по модулю силы F1 и F2 (рис. 170), приводят рычаг в движение. При этом оказывается, что заодно и то же время точка приложения меньшей силы F2 проходит больший путь s2, а точка приложения большей силы F1 — меньший путь s1. Измерив, эти пути и модули сил, находят, что длины путей, пройденных точками приложения сил на рычаге, обратно пропорциональны силам:
s1/s2 = F2/F1
Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько, же раз проигрываем в длине пути.
Произведение силы на путь есть работа. Наши опыты показывают, что работы, совершаемые на обоих концах рычага, равны друг другу:
F1s1 = F2s2
т.е.
A1 = A2
Итак, при использовании рычага выигрыша в работе не получают.
Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Если мы силу приложим к длинному плечу, то выиграем в силе, но во столько же раз проиграем в расстоянии. Действуя же силой на короткое плечо рычага, мы выиграем в расстоянии, но во столько же раз проиграем в силе.
Существует легенда, что Архимед, восхищенный открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я подниму Землю!»
Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали точку опоры и рычаг нужной длины. Для подъема Земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например со скоростью 1 м/с, потребовались бы миллионы лет.
Не дает выигрыша в работе и разновидность рычага — неподвижный блок, в чем легко убедиться на опыте. Пути, проходимые точками приложения сил P и F, одинаковы, одинаковы и силы, а значит, одинаковы и работы.
Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец веревки, к которому прикреплен динамометр, как показывает опыт (рис. 171), переместить на 2h. Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути,— следовательно, и подвижный блок не дает выигрыша в работе.
Многовековая практика показала, что ни один из механизмов не дает выигрыша в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.
Уже древним ученым было известно правило, применимое ко всем механизмам: во сколько раз выигрываем в силе, во столько раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.
Вопросы. 1. Какое соотношение существует между силами, действующими на рычаг, и плечами этих сил? 2. Какое соотношение существует между путями, пройденными точками приложения сил на рычаге, и этими силами? 3. Можно ли при помощи рычага получить выигрыш в силе? В чем тогда проигрывают? 4. Во сколько раз проигрывают в пути, используя для поднятия грузов подвижный блок? 5. В чем состоит «золотое правило» механики?
Упражнения.
- С помощью подвижного блока груз подняли на высоту 1,5 м. На какую длину при этом был вытянут свободный конец веревки?
- С помощью подвижного блока подняли груз на высоту 7 м. Какую работу совершил рабочий при подъеме груза, если он прилагал к концу веревки силу 160 Н? Какую работу совершит рабочий, если поднимет этот груз на высоту 7 м без блока? (Вес блока, и силу трения не учитывать.)
- Как применить блок для выигрыша в расстоянии?
- Как можно соединить друг с другом неподвижные и подвижные блоки, чтобы получить выигрыш в силе в 4 раза? в 6 раз?
Задание.
Докажите, что закон равенства работ («золотое правило» механики) применим к гидравлической машине. Трение между поршнями и стенками сосудов не учитывайте.
Указание. Используйте для доказательства рисунок 132. Когда малый поршень под действием силы F1 опускается вниз на расстояние h1 он вытесняет некоторый объем жидкости. На столько же увеличивается объем жидкости под большим поршнем, который при этом поднимается на высоту h2.