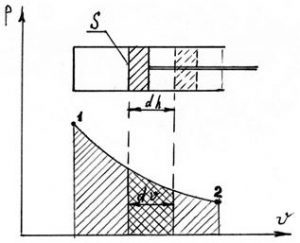
Рис. 6.2. Изображение работы в pv-диаграмме при переменном давлении в системе
Пусть происходит процесс 1-2 расширения рабочего тела массой 1 кг в цилиндре. Если площадь поршня S, то при перемещении dh он совершает работу pSdh:
dl = pSdh, Дж (6.42)
где pS – сила, Н
dh –путь, м
В то же время Sdh = dV, м3 и тогда работу можно представить в виде:
dl = pdV, (6.43)
Если в процессе участвуют m кг газа, то при изменении объёма от V1 до V2 работу можно вычислить интегрируя (1.43):
При аналитическом решении для вычисления интеграла необходима зависимость p=f(v). Для решения задачи в графической форме используется кривая 1-2 в p-v координатной сетке. Площадь под кривой процесса в p-v диаграмме измеряет работу расширения газа. Из рисунка 6.1 видно, что работа (и расширения, и сжатия) зависит не только от начального и конечного состояния газа, но и от характера термодинамического процесса.
Первый закон термодинамики с учётом (6.43) можно представить в виде:
dq = hu + pdV, (6.45)
Здесь du – изменение внутренней энергии.
При термодинамическом преобразовании тепла в работу величиной внутренней энергии считают тот запас энергии, который обуславливается тепловым движением молекул. Внутренняя энергия складывается из кинетической энергии поступательного и вращательного движения молекул и энергии внутри молекулярных колебаний.
Экспериментальные исследования показали, что внутренняя энергия не зависит от давления, объёма или характера термодинамического процесса, а зависит только от температуры, т. е. является функцией состояния. Поэтому для всех термодинамических процессов изменение внутренней энергии можно определить, зная начальную и конечную температуру:
Возвращаясь к первому закону термодинамики записанному в виде (6.45) и рассматривая член уравнения pdV можно увидеть, что pdV является частью дифференциала:
d(pV) = pdV + Vdp, (6.47)
Отсюда pdV можно представить:
pdV = d(pV) — Vdp, (6.48)
Подставив (6.48) в выражение (6.45) получим:
dq = du + d(pV) — Vdp = d (u + pV) — Vdp, (6.49)
В практике тепловых расчётов функций (u+pV) называют энтальпией. Удельная энтальпия (т.е. энтальпия 1 кг рабочего тела) обозначается h (ранее обозначалось i). И так как все параметры, определяющие энтальпию, являются параметрами состояния, энтальпия также параметр состояния. Как и внутренняя энергия энтальпия зависит только от температур: