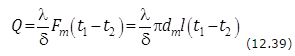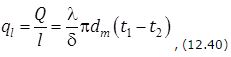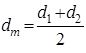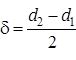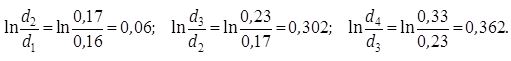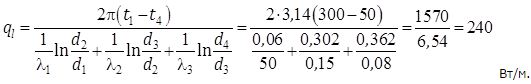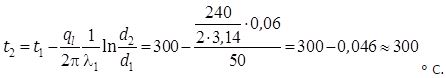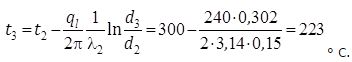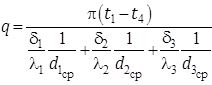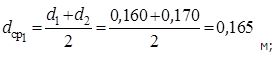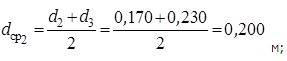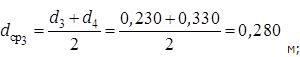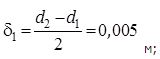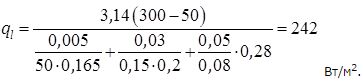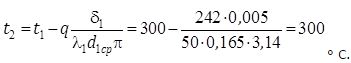Упрощение расчетных формул

Зависимости  для однослойной стенки удобно представить в виде

и

где d_m — средний диаметр, ,

d — толщина стенки трубы, .

При соотношении 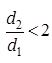формулы (12.39), (12.40) дают погрешность менее 2 %, но при этом значительно упрощают проведение расчетов.

Задача 1.Паропровод диаметром dн = 0,17 м, dвн = 0,16 м покрыт двухслойной изоляцией. Толщина первого слоя изоляции d₂ = 0,03 м, второго — d2 = 0,05 м. Теплопроводность трубы l₁ = 50 Вт/(м·град); первого слоя изоляции — l₂ = 0,15 Вт/(м·град); второго слоя изоляции — l = 0,08 Вт/(м·град). Температура внутренней поверхности трубы t₁ = 300 °C, внешней поверхности изоляции — t₄ = 50 °C. Определить теплопотери одного погонного метра трубопровода и температуры на поверхностях раздела.

Задачу можно решить по традиционной и по упрощенной методикам. Для решения задачи традиционным способом определяем величины натуральных логарифмов:

Теплопотери одного метра составят

Температура на стыке труба – первый слой изоляции:

Температура на стыке первый – второй слои изоляции:

Задача 2. Ту же задачу решить по упрощенной методике.

Так как для всех слоев 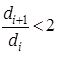, можно применить формулу теплопроводности плоской стенки:

,

где 

d₂ = 0,03 м;

d₂ = 0,05 м;

Температура на стыке труба — первый слой изоляции:

Температура на стыке первый-второй слои изоляции:

Как видно из результатов, погрешность при расчёте по упрощенной методике оказывается исчезающе малой.