Закон инерции для твердых тел

Законы поступательного движения твердых тел, как и любых систем из N частиц, совпадают с первыми двумя законами движения Ньютона, если в них заменить слово «частица» на «центр масс». Если на тело не действуют внешние силы, его центр масс находится в покое или движется равномерно. Однако сами частицы тела не обязательно движутся при этом равномерно. Тем не менее они обязаны двигаться таким образом, чтобы движение их центра масс оставалось все время равномерным. Например, частицы могут вращаться вокруг центра масс; если смотреть на это движение из центра масс, оно будет выглядеть как простое изменение ориентации тела, но не его формы. Это утверждение иллюстрирует фото 8. Центр масс гаечного ключа отмечен черным крестиком. Движущийся по инерции ключ фотографировали через каждую 1/30 с. С помощью линейки можно убедиться в том, что:

• центр масс (т. е. черный крестик) движется по прямой линии;
• он проходит равные расстояния между каждой съемкой.

Сам ключ вращается вокруг центра масс. Если смотреть только на ключ и отвлечься от его перемещения в пространстве, можно представить, что ключ вращается вокруг центра масс, как если бы сквозь центр масс проходила неподвижная ось.

Второй закон движения для твёрдых тел

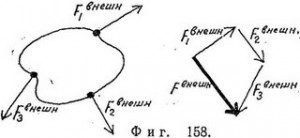
Если на твердое тело действуют внешние силы, то его центр масс ведет себя следующим образом. Условившись, как и ранее, называть сумму всех внешних сил, действующих на тело, результирующей, или полной, внешней силой (фиг. 158):

и применяя к данной задаче теорему 13.2 (центр масс системы из N частиц подчиняется второму закону Ньютона в следующей формулировке: полная внешняя сила = (полная масса) * (ускорение центра масс)), доказанную ранее для общего случая системы из N частиц, получаем, что полная сила, действующая на твердое тело, равна произведению массы тела на ускорение его центра масс:

Этот результат отчасти подтверждает справедливость ньютоновской точки зрения на планеты как на материальные точки. Следует только иметь в виду, что вокруг Солнца обращаются по эллиптическим орбитам, удовлетворяющим трем законам Кеплера, не планеты, а их центры масс. Сами же планеты вольны совершать и другие движения, например, Земля вращается вокруг собственной оси и, подобно волчку, прецессирует.

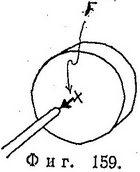
Пример. Предположим, нам необходимо посадить на ось тяжелое колесо так, чтобы его вращение вызывало минимальные вибрации этой оси (фиг. 159). Из сказанного ранее сразу же можно заключить, что ось должна проходить через центр масс (который в случае обычного маховика практически совпадает с его геометрическим центром). Если ось проходит через центр масс, то, с какой бы скоростью ни вращалось колесо, центр масс остается неподвижным; поэтому со стороны оси на колесо не действуют никакие силы.

Так как ось не оказывает воздействия на колесо, то и колесо в соответствии с третьим законом Ньютона не действует на ось и, следовательно, плавно вращается. Если же центр масс не совпадает с осью колеса, то он будет двигаться при вращении колеса. Так как это движение не является прямолинейным, к центру масс должна быть приложена сила. Эта сила может исходить только от оси, поэтому колесо в свою очередь действует с такой же силой на ось. (Чтобы центр масс равномерно вращался вокруг оси, к нему необходимо приложить силу, направленную в сторону оси, подобно тому, как требуется приложить силу для удержания планет, вращающихся вокруг Солнца.) Таким образом, при вращении колеса на ось действует постоянная по величине сила, направление которой поворачивается вместе с колесом, что и вызывает вибрацию оси.