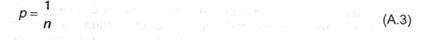В естественных науках изучаются явления, финал которых определяется конкретными причинно-следственными связями, выраженными при помощи математического понятия аргумент-функция. К примеру, электросопротивление цепи и напряжение на ее концах совершенно точно задает силу тока, что является сущностью закона Ома. При этом, сколько раз не повторялся бы опыт, итог измерения силы тока окажется схожим (в границах погрешности измерений).

Но нередко приходится иметь дело с явлениями, финал которых многозначен и находится в зависимости от причин, которые не знаем либо не можем учитывать. Простой и обычный пример — пророчество результата бросания монеты, т.е. выпадение «орла» либо «решки». Схожей же оказывается ситуация с выигрышем по лотерейному билету, получением определенной карты в карточных играх, попадание в цель при стрельбе, итог спортивной встречи, количество пассажиров в автобусе и пр.

Явления, финал которых не может быть совершенно точно определен до того, как они произошли, именуются случайными.

Раздел арифметики, в каком строится понятийный и математический аппарат для описания случайных событий, именуется теорией вероятностей. Количественное описание случайных событий опирается на то, что при неоднократном повторении явления с разноплановым финалом в одних и тех же критериях частота возникновения некого результата остается примерно схожей. Будем именовать отдельный повтор случайного явления опытом, а интересующий финал этого явления — подходящим событием (либо подходящим финалом). Тогда, если N — общее число опытов, а N_A — количество подходящих исходов случайного действия А, то отношение:

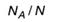
будет демонстрировать долю подходящих исходов в проведенной серии опытов либо относительную частоту возникновения подходящего финала. Но в различных сериях при маленьком количестве опытов в каждой значение частоты возможно окажется различной. К примеру, в серии из 3 опытов по бросанию монеты 2 раза выпал орел и 1 решка. Если подходящим финал считать выпадение сокола, то частота выходит равной 2/3. В другой же серии из 3-х опытов итог возможно окажется совсем другим, к примеру, все 3 раза выпадет решка и, как следует, частота возникновения сокола оказывается равной 0. Частота стремится к некой определенной (и неизменной) величине исключительно в том случае, если количество опытов будет велико, в предельном случае стремиться к бесконечности. Это величина и именуется вероятностью случайного действия А:

Данное определение вероятности именуется частотным; оно применимо для вероятных исходов, образующих дискретный (конечный) набор. Есть и случайный действия, имеющие непрерывный ряд вероятных исходов, к примеру, значение скорости молекулы газа либо время ее пребывания в некой области места; для таких событий употребляется другое определение вероятности. Будем иметь дело только с дискретными событиями и воспользоваться приведенным выше определением.

Непременно, разные действия имеют разную возможность. Можно считать, что значение вероятности охарактеризовывает событие и, в то же время, является его функцией; по этой причине будем придерживаться обозначения р(А).

Кандидатурой случайному событию является событие, относительно которого точно знаем, что оно произойдет (к примеру, пришествие денька после ночи) — такие действия будем именовать достоверными. Достоверное событие можно рассматривать как предельный случай действия случайного — для него в любом опыте N_A — N и, согласно (А.1), р(А) = 1. Напротив, действия, которые никогда не могут произойти — будем именовать их неописуемыми (к примеру, вытащить красноватый шар из урны с белоснежными и темными) — имеют всегда N_A = 0 и, как следует, р(А) = 0. Таким макаром, случайные действия размещаются меж неописуемыми и достоверными, а для их частотной свойства — вероятности — разумеется, будет справедливо соотношение:

Приобретенное выражение именуется условием нормировки вероятностей; в предстоящем получим более общую форму его записи.

Непременно, принципиальной задачей является определение (либо оценка) вероятности некого случайного действия. Но произвести фактически нескончаемое число опытов, что просит определение вероятности, естественно, нереально. Потому приходится завлекать некие другие суждения. Разглядим ситуацию, когда случайное событие имеет несколько независящих исходов, но они все равновероятны, т.е. относительные частоты их пришествия схожи. Пусть п — общее число равновероятных событий, которые обозначим А₁, А₂, … А_п; вероятности их пришествия будут, соответственно, р(A₁), р(А₂), … р(А_п). Разглядим сложное событие А, для которого подходящим окажется хоть какой из исходов А₁, … А_п; разумеется, такое событие будет достоверным (потому что какое-то из перечисленных событий все равно произойдет) и, как следует, возможность сложного действия р(А) = 1. С другой стороны, так как отдельные действия независимы, т.е. пришествие хоть какого из их никак не связано и не обосновано другими, каждое из их занесет свою лепту величиной р(A_i) в возможность сложного действия. Т.е.

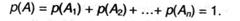
Потому что рассматриваются равновероятные действия, разумеется

Как следует, р(А) = п∙р = 1, откуда получаем, что возможность хоть какого из равновероятных событий будет равна: