Число в системе счисления р с k разрядами, разумеется, будет иметь наибольшее значение в этом случае, если все числа числа окажутся наивысшими, т.е. равными р — 1. Тогда

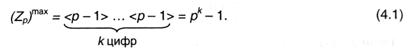
Количество разрядов числа при переходе от одной системы счисления к другой в общем случае изменяется. Разумеется, если р = q^σ (σ — не непременно целое), то (Z_p)^max = p^k — 1 = q^σk — 1. Т.е. количество разрядов числа в системах счисления р и q будут различаться в σ раз. Разумеется соотношение:

При всем этом основание логарифма никакого значения не имеет, так как σ определяется отношением логарифмов. Сравним количество цифр в числе 99₁₀ и его представлении в двоичной системе счисления: 99₁₀ = 1100011₂; т.е. двоичная запись просит 7 цифр заместо 2 в десятичной, σ = ln(10)/ln(2) = 3,322; как следует, количество цифр в десятичном представлении необходимо помножить на 3,322 и округлить в огромную сторону: 2-3,322 = 6,644 = 7.

Введем понятие экономичности представления числа в данной системе счисления.

Под экономичностью системы счисления будем осознавать то количество чисел, которое можно записать в данной системе при помощи определенного количества цифр.

Речь в этом случае идет не о количестве разрядов, а об полном количестве сочетаний цифр, которые интерпретируются как разные числа. Поясним на примере: пусть в распоряжении имеется 12 цифр. Можно разбить их на 6 групп по 2 числа («0» и «1») и получить шестиразрядное двоичное число; полное количество таких чисел, как уже не один раз дискуссировалось, равно 2⁶. Можно разбить данное количество цифр на 4 группы по три числа и пользоваться троичной системой счисления — в данном случае полное количество разных их сочетаний составит 3⁴. Аналогично можно произвести другие разбиения; при всем этом число групп обусловит разрядность числа, а количество цифр в группе — основание системы счисления. Результаты разных разбиений можно проиллюстрировать таблицей:

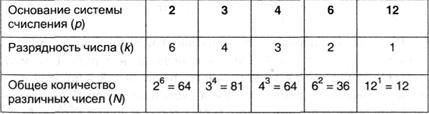
Из приведенных оценок видно, что более экономной оказывается троичная система счисления, при этом, итог будет этим же, если изучить случаи с другим начальным количеством сочетаний цифр.

Четкое размещение максимума экономичности может быть установлено методом последующих рассуждений. Пусть имеется п символов для записи чисел, а основание системы счисления р. Тогда количество разрядов числа k = п/р, а полное количество чисел (N), которые могут быть составлены, равно:

Если считать N(p) непрерывной функцией, то можно отыскать то значение р_т, при котором iN воспринимает наибольшее значение. Функция имеет вид, представленный на рис.4.3.

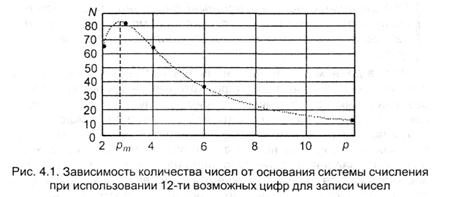
Для нахождения положения максимума необходимо отыскать производную функции N(p), приравнять ее к нулю и решить приобретенное уравнение относительно р.

Приравнивая приобретенное выражение к нулю, получаем ln p = 1, либо р_т = е, где е = 2,71828… — основание натурального логарифма. Наиблежайшее к е целое число, разумеется, 3 — по этой причине троичная система счисления оказывается самой экономной для представления чисел. В 60-х годах в нашей стране была построена вычислительная машина «Сетунь», которая работала в троичной системе счисления. Предпочтение все таки отдается двоичной системе, так как по экономичности она оказывается 2-ой за троичной, а на техническом уровне она реализуется еще проще других. Таким макаром, простота технических решений оказывается не единственным аргументом в пользу внедрения двоичной системы в компьютерах.

4.2.4. Перевод чисел меж системами счисления 2 ↔ 8 ↔ 16

Энтузиазм к двоичной системе счисления вызван тем, что эта самая система употребляется для представления чисел в компьютере. Но двоичная запись оказывается массивной, так как содержит много цифр, и, не считая того, она плохо воспринимается и запоминается человеком из-за зрительной однородности (все число состоит из нулей и единиц). Потому в нумерации ячеек памяти компьютера, записи кодов команд, нумерации регистров и устройств и пр. употребляются системы счисления с основаниями 8 и 16; выбор конкретно этих систем счисления обоснован тем, что переход от их к двоичной системе и назад осуществляется, как будет показано ниже, очень обычным образом.

Двоичная система счисления имеет основанием 2 и, соответственно, 2 числа: 0 и 1.

Восьмеричная система счисления имеет основание 8 и числа 0, 1…..7.

Шестнадцатеричная система счисления имеет основание 16 и числа 0, 1, …, 9, А, В, С, D, Е, F. При всем этом символ «А» является 16-ричной цифрой, соответственной числу 10 в десятичной системе; В₁₆ = 11₁₀; С₁₆ = 12₁₀; D₁₆ = 13₁₀; Е₁₆ = 14₁₀; F₁₆ = 15₁₀. Другими словами, в этом случае А … F — это не буковкы латинского алфавита, а числа 16-ричной системы счисления и потому они имеют только такое начертание (не могут быть представлены в виде, к примеру, соответственных строчных букв, как в текстах).

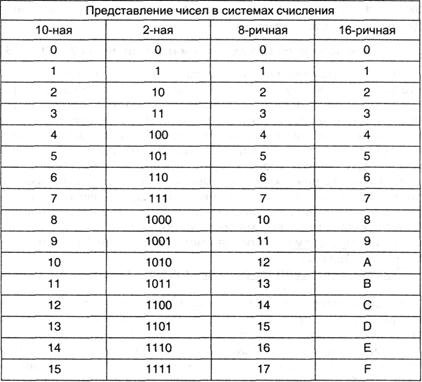
Пользуясь методами, сформулированными в разделе 4.2.1, можно заполнить табл. 4.1.

Докажем две аксиомы.

Аксиома 1. Для преобразования целого числа Z_p → Z_q в том случае, если системы счисления связаны соотношением q = р^r, где r — целое число большее 1, довольно Z_p разбить справа влево на группы по г цифр и каждую из их независимо перевести в систему q.

Подтверждение:

Пусть наибольший показатель степени в записи числа р по форме (4.1) равен k — 1, при этом, 2r > k -1 > r.

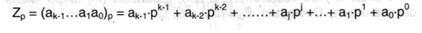
Таблица 4.1.

Вынесем множитель р^r из всех слагаемых, у каких j ≥ r. Получим:

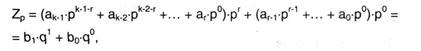
где

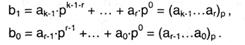
Таким макаром, r-разрядные числа системы с основанием р оказываются записанными как числа системы с основанием q. Этот итог можно обобщить на ситуацию случайного k-1 > r — в этом случае выделится не две, а больше (т) цифр числа с основанием q. Разумеется, Z_q = (b_m … b₀ )_q.