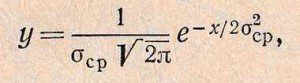Изучение причин (факторов), вызывающих погрешности при обработке заготовок на металлорежущих станках, позволило установить связь между этими причинами и значениями погрешностей и таким образом управлять погрешностями, снижая или устраняя их совсем. В некоторых случаях можно воздействовать на факторы, вызывающие погрешности, так, чтобы они взаимно понижали или ликвидировали отдельные погрешности. Однако так можно поступать, если известен закон действия каждого фактора в отдельности.
В результате совокупного действия всех факторов возникает так называемая результирующая погрешность заданного размера. Эту результирующую погрешность надо знать заранее и не допускать, чтобы ее значение было больше допуска, установленного на заданный размер.
Погрешности в пределах данной совокупности размеров можно разделить на систематические постоянные, т. е. погрешности, имеющие одинаковое значение для всей рассматриваемой совокупности размеров, систематические переменные, закономерно изменяющиеся по ходу технологического процесса, и случайные (погрешности рассеивания), имеющие различные значения при невыясненных причинах их появления.
Так, например, если отверстия у заготовок всей партии обработаны разверткой, имеющей неправильный размер, то погрешность диаметра отверстия является систематической, имеющей постоянный характер. Так как развертка в процессе работы подвергается износу, то и размер отверстия при переходе к обработке каждой последующей заготовки будет закономерно изменяться, при этом погрешность будет систематической с переменным характером. Однако при обработке отверстий заготовок одной и той же разверткой в номинально одинаковых условиях размеры этих отверстий будут все-таки неодинаковы в результате действия ряда факторов (различие в твердости и т. п.), иначе говоря, получается рассеивание размеров отверстий заготовки, которые характеризуются погрешностями рассеивания, имеющими случайный характер.
Для определения результирующей погрешности необходимо суммировать все погрешности по размеру и знаку. В зависимости от характера погрешностей — систематического или случайного — их суммируют различными способами. Систематические постоянные погрешности суммируют алгебраически (с учетом их знаков), что в результате может привести как к увеличению, так и к уменьшению погрешностей или к их компенсации. Систематические переменные погрешности любого знака («+» или «—») суммируют арифметически, причем при определении суммарной погрешности исходят из наименее ВЫГОДНЫХ условий. К этому виду погрешностей относятся: погрешности формы обрабатываемой заготовки, зависящие от жесткости технологической системы; погрешности, связанные с износом инструмента; погрешности настройки станка. Случайные погрешности суммируют по правилу квадратного корня. При симметричном распределении составляющих погрешностей результирующая погрешность:
где k1, k2, k3, …, km— коэффициенты, зависящие от вида кривых распределения составляющих погрешностей; ∆1, ∆2, ∆3, …, ∆m— независимые случайные погрешности.
Если все составляющие погрешности следуют одному закону распределения, то k1=k2=k3=…=km=k. Наименьшая результирующая погрешность бывает тогда, когда составляющие погрешности следуют закону нормального распределения (k=1). При износе инструмента результирующая погрешность возрастает (k=1,2… 1,5), а при большом износе кривая распределения составляющих погрешностей следует уже закону равной вероятности (k=1,7). При работе на предварительно настроенных станках с автоматическим получением размеров и незначительным износом режущего инструмента распределение большинства случайных погрешностей близко к закону нормального распределения.
Основными характеристиками распределения случайной погрешности являются: средний размер и среднее квадратичное отклонение. Понятие среднего размера относится к любому параметру — диаметру, длине, угловому размеру, отклонению от параллельности, плоскостности, перпендикулярности, соосности и т. д. Средний размер определяют по формуле:
Lcp = (L1 + L2 + L3 + … + Ln)/n;
где L1, L2, L3, …, Ln — размеры отдельных заготовок или деталей; n— общее количество заготовок или деталей в партии. Среднее квадратичное отклонение определяют по формуле:
Опытные кривые можно заменить математическими кривыми, характеризующими определенные законы распределения случайных погрешностей. Так, уравнение кривой нормального распределения (кривой Гаусса с ординатой у) имеет вид:
где σср — среднее квадратичное отклонение; х=Li— Lcp; е=2,718 — основание натуральных логарифмов.
 На рис. 10 приведены кривые нормального распределения для значений σср=0,5; σср=1 и σср=2. Зависимость формы кривой распределения от значения среднего квадратичного отклонения характеризует рассеивание. Чем меньше значение σср, тем меньше рассеивание и кривая имеет суженную форму, а при большем σср рассеивание размеров выражается резней кривая имеет растянутую форму.
На рис. 10 приведены кривые нормального распределения для значений σср=0,5; σср=1 и σср=2. Зависимость формы кривой распределения от значения среднего квадратичного отклонения характеризует рассеивание. Чем меньше значение σср, тем меньше рассеивание и кривая имеет суженную форму, а при большем σср рассеивание размеров выражается резней кривая имеет растянутую форму.
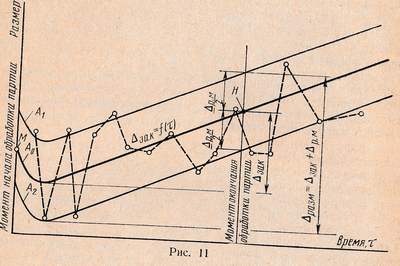
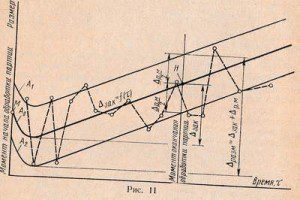
Для практических целей и характеристики точности операции в течение времени обработки применяют диаграмму точности обработки (рис. 11), которую строят в следующем порядке. Вначале строят линию изменения размера А0. Для этого определяют составляющие систематических погрешностей для ряда моментов времени. Суммируя (алгебраически) эти погрешности, находят общую систематическую погрешность как функции времени: ∆зак = ƒ(τ). По обе стороны от линии А0 откладывают значения мгновенного рассеивания ∆р.м/2 или поля рассеивания при настройке ∆р.н/2, которые образуют две кривые А1 и А2 (расчетное поле рассеивания). Тогда ∆разм=∆зак+∆р.м; ∆разм= ∆зак+∆р.н (при настройке).
 Построение диаграммы основано на предварительном расчете при заданном значении поля рассеивания и построении линии изменения размера по принятой теоретической закономерности изменения суммарной погрешности.
Построение диаграммы основано на предварительном расчете при заданном значении поля рассеивания и построении линии изменения размера по принятой теоретической закономерности изменения суммарной погрешности.
При исследованиях на диаграмму наносят точки, полученные в результате эксперимента. Их размещение внутри расчетного поля свидетельствует о правильности построения диаграммы. В тех случаях, когда распределение случайных погрешностей подчиняется закону нормального распределения, в интервале ±0,3σср находится около 25% размеров деталей партии, в интервале ±0,7σср — около 50% размеров, в интервале ±1,1σср — около 75% и, наконец, в интервале ±3σср — около 99,7% всех размеров.
При определении рассеивания расчетным путем полное значение мгновенного рассеивания складывается из рассеивания, не зависящего от нагрузки ∆р. м. незав и зависящего от нагрузки ∆р. м нагр, или:
Величина ∆р.м.незав без учета погрешностей формы при повышенной точности обработки (при чистовом точении) составляет 6…19 мкм, а при обычной точности 11…35 мкм. Величину ∆р.м.нагр можно определить по формуле:
∆р.м.нагр = 1.2(∆р. заг /k)
где ∆р. заг — рассеивание размеров заготовок, равное 0,1z (z — припуск на диаметр); k — коэффициент, учитывающий свойства обрабатываемого материала.
Построение диаграммы должно быть увязано с размерами детали на чертеже. Для этого определяется положение начальной точки М (рис. 11), соответствующее началу обработки партии деталей. Эта привязка осуществляется настройкой на размер с обеспечением совпадения середины поля рассеивания всей партии деталей с серединой поля допусков δ. Точка H соответствует окончанию обработки партии деталей. Разность абсцисс точек H и М равна промежутку времени между двумя поднастройками станка.