Периодическая таблица элементов. Принцип запрета играет фундаментальную роль при интерпретации периодической таблицы Менделеева. Если бы этого принципа не существовало, волновые функции первых нескольких атомов выглядели бы так, как показано на фиг. 190. Штриховкой отмечены здесь те области пространства, где квадрат волновой функции, а, следовательно, и вероятность нахождения электрона достаточно велики. Таким образом, если бы принципа запрета не было, увеличение числа положительных зарядов приводило бы лишь к тому, что каждый новый электрон стремился бы попасть в наинизшее 1S-состояние. Так, в атоме, ядро которого содержит, скажем, N положительных зарядов, состояние каждого из N электронов было бы эквивалентно 1S-состоянию этого атома. Такие атомы обладали бы совершенно иными химическими свойствами, чем реально существующие атомы, причем на основании приведенных рассуждений было бы трудно ожидать, что свойства атомов могут резко изменяться при переходе от одного атома к следующему. Известно, однако, что гелий, атомы которого состоят из двух положительных зарядов и двух электронов, является благородным газом, причем настолько инертным, что он практически не соединяется ни с одним из элементов1). Литий же, атомы которого содержат три положительных заряда, является очень активным щелочным металлом. Для перехода от благородного газа к щелочному металлу — от одного из наиболее инертных элементов к наиболее активному — потребовалось лишь добавление одного положительного заряда в ядре и одного электрона во внешней оболочке.
1) Недавно химикам после столетних усилий удалось получить соединения благородных газов.
Чтобы перейти от фтора (настолько активного, что его соединение с водородом — плавиковая кислота—растворяет даже стекло) к инертному неону, другому благородному газу, достаточно в ядро атома фтора добавить один положительный заряд, а в его внешнюю оболочку — один электрон. Если добавить еще один положительный заряд и еще один электрон, то мы получим атом элемента натрия, настолько активного, что он ярко вспыхивает при соприкосновении с водой.
Трудно было бы объяснить эти и другие закономерности периодической таблицы, если бы все электроны были сосредоточены вблизи ядра, находясь в наинизшем состоянии. Пытаясь объяснить периодическую таблицу, Бор еще до появления принципа запрета и введения уравнения Шредингера выдвинул предположение, что на основном уровне могут находиться только два электрона, на втором уровне — восемь электронов и т. д. Хотя это предположение не совсем соответствует современным представлениям, оно тем не менее довольно близко к ним и позволяет воспроизвести набор атомов, который обладает некоторыми качественными чертами периодической системы элементов (фиг. 191).
С точки зрения уравнения Шредингера и принципа запрета заполнение периодической таблицы происходит следующим образом. Атом первого элемента, водорода, состоит из одного протона и одного электрона, находящегося в 1S-состоянии (фиг. 192). Атом второго элемента, гелия, содержащий два положительных заряда, имеет два электрона в 15-состоянии, что допустимо, так как их спины могут быть направлены в противоположные стороны (фиг. 193). Однако при переходе к атому лития, содержащему три положительных заряда, квантовые числа, соответствующие 1S-состоянию, оказываются «занятыми», поэтому третий электрон необходимо помещать дальше от ядра и приписывать ему 2S-состояние (фиг. 194). Так как энергия связи в состоянии 2S меньше, чем в состоянии 1S, этот последний электрон слабее связан с ядром, чем первые два электрона. Гелий является наиболее инертным элементом из всех благородных газов; чтобы высвободить электрон из атома гелия, требуется энергия порядка 24,6 эВ, тогда как, чтобы удалить внешний электрон из атома лития, требуется всего лишь 5,4 эВ. Отсюда ясно, почему в химических реакциях, в которых всегда происходит переход электронов от атома одного элемента к атому другого элемента, гелий ведет себя значительно пассивнее, чем литий.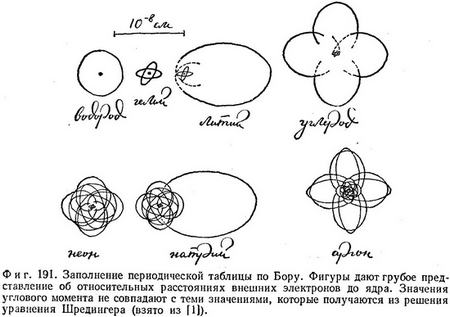
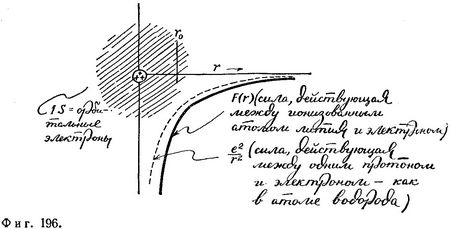
Приведенный выше анализ был бы абсолютно точным, если бы электроны не взаимодействовали между собой. Они просто заполняли бы уровни с различными квантовыми числами, характерными для атома водорода, и с соответствующими значениями энергии, как это было в случае невзаимодействующих частиц, заключенных в одномерном сосуде. Наличие же взаимодействия приводит к некоторому изменению характера силы, приложенной к каждому из электронов. Например, третий электрон атома лития, находясь вдали от этого атома, чувствует силу лишь со стороны одного положительного заряда (два других положительных заряда заэкранированы двумя электронами, находящимися в 1S-состоянии); когда же он находится вблизи ядра (внутри 1S-оболочки), на него действует гораздо большая сила со стороны трех положительных зарядов ядра (фиг. 195). Таким образом, вдали от ядра на электрон действует примерно такая же сила, какая действует на электрон со стороны протона (как в атоме водорода), вблизи же ядра на него действует гораздо большая сила (фиг. 196).
Хотя зависимость этой силы от г отличается от кулоновской, сама сила остается приблизительно сферически симметричной. (Соответствующие эквипотенциальные поверхности имеют сферическую форму.) Поэтому структура вырождения уровней остается прежней, несмотря на то что положение самих уровней может слегка измениться. Следовательно, мы можем по-прежнему пользоваться квантовыми числами водородного атома (n, l, ml и ms), помня, что теперь они характеризуют сферически симметричную силовую систему, соответствующую ионизованному атому лития, и что точное положение энергетических уровней не обязательно совпадает с положением уровней атома водорода. Этот случай является классическим примером того, как, не решая уравнения Шредингера, но зная симметрию силовой системы, можно без труда описать соответствующую структуру вырождения уровней. В качестве примера смещения уровней рассмотрим 2S- и 2Р-состоя-ния. Энергии этих состояний в атоме водорода совпадают. В атоме же лития энергия 25-состояния несколько меньше. Это можно объяснить тем, что волновая функция 2S-состояния сосредоточена в среднем ближе к ядру, чем волновая функция 2Р-состояния. В результате в 2S-состоянии на электрон в случае атома лития действует большая сила, чем в случае атома водорода (три положительных заряда в ядре лития находятся внутри оболочки из двух электронов в 15-состоянии), поэтому волновой функции этого электрона соответствует меньшее значение энергии.
Таким образом, заполняя периодическую таблицу, мы продолжаем использовать квантовые числа n, l, ml и ms. Мы полагаем, что все 2l+1 уровней, соответствующих заданному значению углового момента, окажутся вырожденными (квантовые числа и характер вырождения такие же, как в случае одного электрона, находящегося в сферически симметричной силовой системе), однако их расположение может быть смещенным относительно энергетических уровней атома водорода.
Добавляя еще один положительный заряд в атомное ядро и еще один электрон в 2S-состоянии, мы получаем следующий элемент — бериллий. Потенциал ионизации бериллия (энергия, необходимая для удаления из атома одного электрона) равен 9,3 эВ. Он выше потенциала ионизации лития, так как в атоме бериллия добавился положительный заряд, притягивающий электроны. Таким образом мы заполнили как состояние 1S, так и состояние 2S. Далее следуют ЗX2-кратно вырожденные уровни состояния 2Р2). На этих уровнях могут находиться шесть электронов, причем у трех из них спины будут направлены вверх, а у оставшихся трех — вниз. (Спин электрона играет решающую роль в удвоении числа возможных уровней.) электрон в 2Р-состоянии связан с атомом несколько слабее, чем, будь это возможно, третий электрон на уровне 2S; поэтому потенциал ионизации бора, атома с пятью электронами, равен 8,3 эВ и оказывается несколько ниже потенциала ионизации атома бериллия (9,3 эВ).
После бора потенциал ионизации начинает снова расти, так как увеличивающийся положительный заряд ядра все сильнее притягивает к себе электроны: 6 электронов, углерод, 11,3 эВ; 7 электронов, азот, 14.5 эВ; при восьми электронах, кислород, он снова спадает до 13,6 эВ; далее 9 электронов, фтор, 17,4 эВ; и, наконец, 10 электронов, неон, 21.6 эВ — благородный газ и завершающий элемент этой серии. Следующий электрон уже не может находиться в состояниях 1S, 2S и 2Р. Все эти состояния заполнены. Поэтому мы должны взять следующее значение главного квантового числа n=3; соответствующие уровни находятся дальше от ядра, чем уровни с n=2, поэтому электроны на уровнях с n=3 слабее связаны с атомом, чем электроны на уровнях с n=2. Первым идет уровень 3S. Потенциал ионизации атома с 11 электронами, натрия, равен 5,1 эВ.
2) Три уровня соответствуют значениям ml =0, 1, —1, в каждом из которых спиновое число может иметь два значения: ms = 1/2 или —1/2 всего получаем 3X2=6 уровней.
Аналогичным образом можно до конца заполнить всю периодическую таблицу. Два уровня состояния 3S дают натрий и магний. Далее следует ЗX2-кратно вырожденное ЗР-состояние. Этим уровням соответствуют элементы алюминий, кремний, фосфор, сера, хлор и аргон. Атом хлора чрезвычайно активен, так как требуется добавление всего лишь одного электрона, чтобы получился инертный элемент аргон, у которого электронная оболочка заполнена.
После аргона можно было бы ожидать, что начнут заполняться уровни 5X2-кратно вырожденного ЗD-состояния. Однако подобно тому, как энергия связи электронов в ЗР-состоянии была меньше энергии связи электронов в 3S-состоянии, энергия связи в ЗD-состоянии оказывается меньше, чем энергия связи электронов в ЗР-состоянии, и даже немного меньше энергии связи в следующем, 4S-состоянии. Поэтому внешние электроны следующих элементов, калия и кальция, находятся в 4S-состоянии, и свойства этих элементов сходны со свойствами натрия и магния, внешние электроны которых находятся в 3S-состоянии. Далее заполняются уровни 3D. Соответствующие элементы обладают той особенностью, что при их ионизации выбиваются не ЗD-электроны, а электроны, находящиеся на уровне 4S. Поэтому потенциалы ионизации всех этих «переходных элементов», как называют элементы, в которых происходит заполнение D-оболочек, приблизительно одинаковы (порядка 7 эВ), а химические свойства этих элементов весьма сходны между собой. Всего в этой группе таких переходных элементов 10.
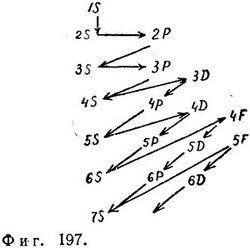
После цинка, последнего из переходных элементов, соответствующих заполнению ЗD-оболочки, следуют элементы, в которых заполняется 4Р-оболочка (ЗX2-кратно вырожденное состояние) и которые заканчиваются криптоном, еще одним инертным газом, атомы которого содержат два 1S-электрона, два 2S-электрона, шесть 2Р-электронов, два 3S-электрона, шесть ЗР-электронов, два 4S-злектрона, десять ЗD-электронов и шесть 4Р-электронов — всего 36 электронов. В периодической таблице есть еще около семидесяти элементов. За некоторыми исключениями, уровни энергии всех элементов заполняются в следующем порядке: 1S, 2S, 2Р, 3S, 3Р, 4S, 3D, 4Р, 5S, 4D, 5Р, 6S, 4Р, 5D, 6Р, 7S, 5P, 6D. На фиг. 197 представлена диаграмма последовательного заполнения периодической таблицы.
Химическое сходство некоторых элементов в периодической таблице объясняется теперь сходством волновых функций их внешних электронов. Например, у всех щелочных металлов, химически очень активных элементов, соответствующих началу заполнения новой оболочки (новому значению главного квантового числа), внешний электрон находится в S-состоянии и расположен достаточно далеко от «остова» атома, в результате чего величина его энергии связи оказывается сравнительно низкой. Такой структурой обладают атомы лития, натрия, калия, рубидия, цезия и франция; все эти элементы чрезвычайно активны. В группу галогенов (элементов, сходных с фтором) входят фтор, хлор, бром, йод и астат, у атомов которых не хватает одного электрона для заполнения Р-оболочки. Далее, благородные газы — гелий, неон, аргон, криптон и ксенон (они очень редко соединяются как друг с другом, так и с другими элементами) — характеризуются тем, что электронные оболочки их атомов заполнены до конца, а следующие уровни лежат довольно далеко, так что к ним не могут присоединиться дополнительные электроны.
Представляет также интерес рассмотреть большие периоды элементов, такие как группа переходных элементов ЗD, куда входят элементы со сходными свойствами. Элементы, в которых заполняется оболочка 4D, химически сходны с элементами группы 3D. Четырнадцать элементов, соответствующих заполнению оболочки 4F (такие состояния 7X2-кратно вырождены), похожи друг на друга, и поскольку они не очень распространены в природе, их называют редкоземельными элементами. За ними следуют элементы группы 5D, свойства которых во многих отношениях напоминают свойства переходных элементов групп 3D и 4D. Последней группе элементов в периодической таблице соответствует заполнение оболочек 5F и 6D. Первые четыре элемента этой группы называются актинидами, к актинидам относятся актиний, торий, протактиний и уран. Эти элементы, как и редкоземельные элементы, обладают практически одинаковыми химическими свойствами. После урана идут трансурановые элементы.
Таким образом, нам удалось, по крайней мере качественно, объяснить основные свойства периодической системы элементов. Однако ясно, что в процессе анализа периодической системы мы использовали целый ряд определенных допущений. Никому еще не удалось получить точное решение уравнения Шредингера даже в случае двухэлектронного атома гелия. Говорить же о точном решении уравнения Шредингера в случае многоэлектронных систем не приходится, даже если для этого мы привлечем самые современные вычислительные машины и все известные в настоящее время методы счета. Поэтому мы вынуждены при исследовании таких систем, как и при исследовании классических или любых логических систем, когда следствия из правил оказываются слишком сложными, чтобы их можно было вывести из исходных постулатов, вводить какие-то разумные допущения, согласующиеся со всем известным ранее.
Основное предположение, использованное при анализе периодической таблицы, состоит в том, что сила, действующая на отдельный электрон (со стороны ядра и остальных электронов системы), считается инвариантной относительно поворотов (т. е. сферически симметричной). В результате характер вырождения уровней, оказывается следствием сферической симметрии, что и позволяет объяснить большинство качественных свойств элементов. Взаимное расположение невырожденных уровней (1S, 2S, 2Р, …) определяется точной радиальной зависимостью потенциала. Распределение же потенциала вычисляется с помощью так называемого самосогласованного метода. Сначала вид потенциала задают, затем, используя этот потенциал, вычисляют уровни энергии и соответствующие волновые функции; далее с помощью полученных волновых функций (поскольку квадрат волновой функции дает распределение отрицательного заряда) определяют новый электрический потенциал. Если этот потенциал совпадает с исходным, то считают, что он соответствует возможному решению уравнения Шредингера, а само решение является самосогласованным. На основании общей согласованности всех известных результатов можно считать, что квантовая физика в современном ее виде правильно объясняет периодическую систему элементов.