Понятно, что развитие живого организма есть последовательность автономных актов самоорганизации. Управление этим процессом может осуществляться при помощи слабеньких воздействий, которые оказывают влияние на выбор того либо другого определенного пути развития в те моменты, когда развивающаяся структура оказывается в состоянии «бифуркации», характеризующегося наличием нескольких вероятных равноправных продолжений. Конкретно эти слабенькие управляющие воздействия закодированы, по всей видимости, в генетических последовательностях первичной клеточки.
Внедрение таких принципов в технике позволило бы резко расширить ее способности, строить ее «в формах самой жизни». Это привело бы к преодолению нынешних принципных различий меж миром техники и миром живой природы. Одни и те же закономерности должны лежать в базе функционирования искусственно сделанных технических устройств и живых организмов.
Активные среды характеризуются непрерывным притоком энергии от наружного источника и ее диссипацией. Благодаря тому, что через каждый на физическом уровне малый элемент среды протекает поток энергии, этот элемент выводится из состояния равновесия и приобретает способность совершать автоколебания, быть бистабильным (триггерным) либо возбудимым. Когда такие элементы локально связаны меж собой и сформировывают определенную структуру, то в таковой среде наблюдается образование стационарных либо зависящих от времени пространственных структур. Такие процессы лежат в базе явления самоорганизации в активных средах.
Исследование такового кооперативного поведения в физических системах является принципиальной составной частью физикиконденсированных систем. Но рассматриваемые при всем этом системы владеют специфичностью, не характерной биологическим либо сложным хим системам, потому что элементы, из которых состоят такие физические системы, являются пассивными.
Для биологии типична другая ситуация, тут отдельными элементами могут быть активными, к примеру, живы клеточки, мельчайшие организмы и т.п. Сохранение активности таких систем может быть только благодаря притоку энергии от наружных источников. При всем этом выделяют три простых типа активных частей:
- бистабильные,
- возбудимые,
- автоколебательные.
Можно провести аналогию меж апериодическим, бифуркационным и колебательным процессами в сложных динамических системах. К примеру, в многоосцилляторных системах аналогом таких режимов могут являться три вида их динамических состояний, к примеру, синхронный, бифуркационный и асинхронный режимы связанных колебаний в системах различной трудности.
Бистабильный либо триггерный элемент обладает 2-мя стационарными состояниями, в каждом из которых он может находиться неограниченно длительно. Наружные воздействия могут приводить к переходам из 1-го состояния в другое. Чтоб вызвать такие переходы, интенсивность воздействий должна превосходить некие пороговые уровни.
Возбудимый (мультивибраторный) элемент имеет единственное выделенное состояние покоя, устойчивое по отношению к слабеньким наружным воздействиям. Но таковой элемент отличается от пассивного по собственной реакции на воздействия, превосходящие пороговый уровень. В ответ на довольно насыщенное наружное воздействие в элементе появляется вспышка активности: он совершает переходы и потом ворачивается в состояние покоя.
Автоколебательный элемент работает подобно «вечному двигателю». Он автономно совершает циклические переходы через некую группу состояний. Наружные воздействия способны только замедлить либо ускорить эти циклические движения, но не остановить их.

Рис. 13.1 Схема распространения волны переключения в цепочке из бистабильных частей. Показаны состояния частей цепочки в поочередные моменты времени 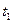 ,
, 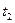
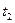
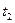
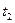
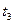
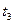
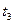
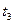
На рисунке представлена цепочка из бистабильных частей. В ней воздействие друг на друга оказывают только примыкающие элементы. При этом, если они находятся в схожем состоянии, то не оказывают воздействия друг на друга. Ведут взаимодействие только тогда, когда их состояния отличаются. Элемент, находящийся в наименее устойчивом состоянии (метастабильным), может перейти в более устойчивое состояние – такое же, как у его соседа. В итоге по цепочке может распространяться волна переключений состояний.
Если цепочка состоит из возбудимых частей, то элемент, перешедший из состояния покоя в активную форму, остается невосприимчивым к наружным воздействиям, пока не совершит всю предписанную ему последовательность переходов. Потому довольно разглядеть только случаи, когда по соседству оказались два элемента, из которых один находится в активной форме, а другой в состоянии покоя. Вероятны два вида их взаимодействия. Во-1-х, всякий элемент в активной форме мог бы выводить из состояния покоя оказавшийся рядом с ним элемент. В данном случае в ответ на однократное воздействие в цепочке появляется незатухающая волновая активность.
Более увлекательная ситуация, когда выводить из состояния покоя могут только элементы, находящиеся в первых фазах вспышки активности. Тогда в итоге возбуждения последнего элемента в цепочке по ней будет распространяться уединенный импульс активности (волна возбуждения), после прохождения которого, элементы ворачиваются в начальное состояние.


Рис. 13.2 Схема распространения волны возбуждения в цепочке из возбудимых частей. Показаны состояния частей цепочки в поочередные моменты времени 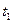
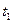
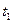
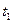
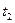
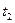
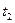
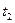
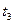
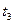
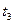
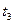
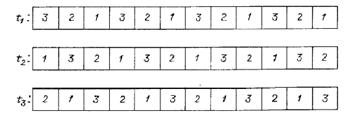

Рис. 13.3 Схема распространения фазовой волны в цепочке из автоколебательных частей. Показаны состояния частей цепочки в поочередные моменты времени 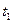
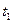
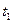
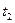
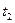
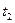
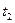
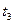
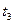
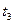
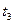
Еще больше сложные эффекты наблюдаются в двумерных либо трехмерных сетях, образованных бистабильными, возбудимыми либо автоколебательными элементами.
В рассматриваемых примерах активные элементы выступают практически в качестве определенных автоматов, т.е. объектов с дискретным набором состояний и некими правилами переходов меж ними. Более детализированный уровень описания основывается на построении дифференциальных уравнений, характеризующих динамику отдельных частей и их взаимодействия.
При переходе от сплошной среды к дискретной, состоящей из набора конечного числа точечных частей, (процессы синхронизации осцилляторов в сложных системах), взаимодействующих меж собой, употребляют понятие клеточных автоматов.
Клеточный автомат (КА) — набор клеток, образующих некую повторяющуюся решетку с данными правилами перехода, определяющими состояние клеточки в последующий момент времени через состояние клеток, находящимися от нее на расстоянии не больше некого, в текущий момент времени. Обычно, рассматриваются автоматы, где состояние определяется самой клеточкой и наиблежайшими соседями. В качестве решетки обычно рассматривается кубическая решетка.
Клеточный автомат состоит из набора объектов (ячеек), обычно образующих регулярную решетку. Состояние раздельно взятого i-го объекта (либо ячейки) в момент времени n характеризуется некой переменной, которая может быть целым, реальным либо всеохватывающим числом, или представлять собой набор из нескольких чисел. Рассматриваемые состояния ячеек меняются синхронным образом через дискретные интервалы времени в согласовании с локальными вероятностными правилами, которые могут зависеть от состояния переменных в ближайших примыкающих узлах. Эти правила не изменяются с течением времени.
Клеточный автомат является дискретной динамической системой, поведение которой стопроцентно определяется в определениях локальных зависимостей. Такая система может оперировать собственной вещественной частью, видоизменять, расширять себя и строить для себя схожих. Довольно знать законы развития системы на микро- либо мезоуровне в маленьких пространственных областях (ячейках), из которых состоит макросистема. Принципиально только, что эти локальные правила схожи для всех ячеек. На новое состояние клеточки могут оказывать влияние только элементы её округи и, может быть, она сама. Ни одна область решётки не может быть отличена от другой по любым особенностям правил и т. п. Но на практике решётка оказывается конечным обилием клеток (ведь нереально выделить неограниченный объём данных). В итоге могут иметь место краевые эффекты, клеточки стоящие на границе решётки будут отличны от других по числу соседей. Огромное количество вероятных состояний клеточки — естественно. Значения во всех клеточках изменяются единовременно, в конце итерации, а не по мере вычисления. В неприятном случае порядок перебора клеток решётки, при совершении итерации, значительно влиял бы на итог.
КА можно поделить на синхронные и асинхронные, детерминированные и вероятностные, подвижные и недвижные, однородные и неоднородные, обыкновенные абстрактные и сложные, точно описывающие реальные системы.
В синхронных КА все клеточки перебегают в новое состояние сразу по сигналу глобального таймера. При всем этом в качестве входных состояний употребляются старенькые состояния примыкающих клеток. В асинхронных КА клеточки перебегают в новое состояние в случайном порядке, при всем этом новое состояние клеточки здесь же может употребляться ее соседями как входное.
Подвижные КА характеризуются возможностью конфигурации положения клеточки в решетке во время эволюции системы. В недвижных КА положение клеточки во время эволюции остается неизменным. КА, в каких состояния ячеек в следующий момент времени определяются на базе неких вероятностей, именуются вероятностными КА (ВКА).
В 2002 году Пауль Чепмен выстроил эталон Жизни в виде РММ (Регистровой Машиной Минского). Практически РММ эквивалентна машине Тьюринга. 1-ая версия эталона была большой (268,096 живых ячеек на площади 4,558 x 21,469 клеток) и неспешной (20 поколений/сек при использовании Life32 Иогана Бонтеса (Johan Bontes) на 400MHz AMD K6-II). Таким образом, в игре Жизнь можно выполнить хоть какой метод, который можно воплотить на современном компьютере.
Способ подвижных клеточных автоматов употребляется для моделирования физико-химических процессов в наноразмерных системах, что связано со сложностью внедрения традиционных способов основанных на решении дифференциальных уравнений.
Понятно, что в неравновесных диссипативных системах при распространении автоволн могут самопроизвольно формироваться постоянные структуры. Такое поведение систем приводит их к самоорганизации, формообразованию. Реальные, сложные нелинейные динамические системы могут характеризоваться очень сложным поведением, именуемым «динамическим хаосом». При всем этом, к примеру, обнаруживаются структуры, схожим образом повторяющие себя. Это свойство самоподобия типично не только лишь для стадии перехода к хаосу, да и в еще большей мере для самих хаотических режимов. Таким образом, динамический хаос представляет собой не только лишь разупорядоченную структуру, но характеризуется в определенном смысле высочайшей степенью регулярности.
Анализ внутренней упорядоченности динамического хаоса приводит к понятию фрактальных множеств. В текущее время фракталы заполучили популярность в связи с тем, что получило самые различные внедрения в физике, химии, астрофизике, гидродинамике, экономике и др. К примеру, теория фракталов может быть применима для исследования функции Вейерштрасса (непрерывная функция, не имеющая производной ни в какой точке).
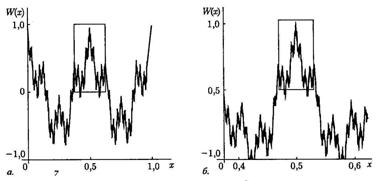

Рис. 13.4 а — график функции Вейерштрасса; б – увеличенная в масштабе часть кривой рисунка (а). Для этой функции кривая воспроизводится на любом сколь угодно малом масштабе (часть подобна целому). К истинному времени понятно огромное число самоподобных множеств.

Рис. 13.5 1-ые шаги построения кривой Пеано, умеренно заполняющей квадрат.
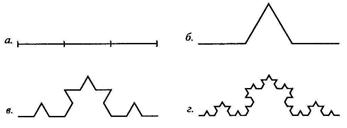

Рис. 13.6 1-ые шаги построения одной из кривых Коха.
Фрактальные структуры появляются и при анализе эволюции нелинейных динамических систем.
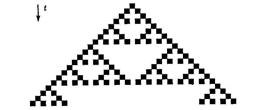

Рис. 13.7 Пример появления фрактальной структуры при работе клеточного автомата.
Задавая автомату метод взаимодействия клеток, можно получить фрактальные огромного количества с определенной внутренней структурой.




Рис. 13.8 Фигуры папоротника и кристалла, порождаемые надлежащими отображениями.
Процессы самоорганизациив нелинейных динамических системах реализуются в разного типа брюсселяторах, нареченных так в честь открывшего их нобелевского лауреата И. Пригожина, проживавшего в Брюсселе. К примеру, традиционным примером самоорганизации систем является появление постоянных структур в подогреваемом снизу слое воды.




Рис. 13.9 Структуры, возникающие в слое воды, нагреваемой снизу.
Рассматривают, к примеру, структуры в виде крутящихся спиральных волн. Такие волны могут появляться и при работе клеточных автоматов.


Рис. 13.10 Спиральные волны в химически активной среде с разными значениями топологических зарядов.
В качестве примера можно привести когерентность химических осциллирующих реакций, протекающих при окислении аммиака и оксида углерода на платине как катализаторе, в неких фотохимических реакциях, и т.п.
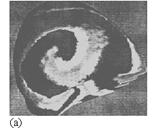



Рис. 13.11 Когерентные процессы в сердечной мышце (а) и в каталитической реакции окисления оксида углерода на платине (б). Чередование светлых и черных областей является индикатором когерентных хим волн.
Био осцилляции есть прямой итог функционирования биохимических осцилляторов. Большой энтузиазм к хим осцилляторам связан с функционированием био ансамблей — клеток, синапсов, нейронов. И 1-ое место тут принадлежит исследованию систем связанных осцилляторов (сердечко — самая «близкая» нам биосистема хим осцилляторов).
В связанных осцилляторах реализуются калоритные предельные режимы: погибель осцилляторов, когда один осциллятор «гасит» другой (инфаркт), «прыжки» от порядка к хаосу (фибрилляции), синтез новейшей частоты либо модуляция частот (тахикардия).
Нельзя также не упомянуть о ярчайшем примере самоорганизованной и самоорганизующейся биохимической системы — мозге, в каком хим и, как следствие, электронная активность синапсов и нейронов синхронизованы. В этом макрореакторе обычным состоянием является порядок, когерентность; хаос — это патологии (типа заболевания Альцгеймера). Безупречный порядок, безупречная когерентность — это генерация мыслей, мыслях и это свойство профессионального, превосходного разума. И чем выше когерентность, тем ярче гениальность — идея не доказанная, но схожая на правду.
Применение данных моделей позволяет изучить динамику возбуждения сложных динамических процессов в почти всех системах различной природы. Данные модели могут быть применены для разработки и совершенствования измерительных устройств последнего поколения, для разработки систем передачи и обработки измерительной инфы, основанных на реализации сложных динамических процессов в осцилляторных системах.
В текущее время у нас в стране и за рубежом проводятся теоретические и экспериментальные исследования пространственно-временной динамики ансамблей, состоящих из активных частей нейродинамического типа. Подобно реальным нейронным ансамблям, такие системы представляют собой сети взаимодействующих частей — «нейронов», локализованных в пространстве.
В отличие от узнаваемых «формальных» нейронных сетей, в нейродинамических системах элемент обладает своей, в неких случаях нетривиальной динамикой. Исследованы явления структурообразования, распространения нелинейных волн, формирования фазовых кластеров, фрактальных пространственно-временных структур динамической активности (рис. ) и др.
Исследуются явления коллективной динамики малых ансамблей связанных генераторов с фазовым управлением — фазовых систем: процессы генерации хаотически модулированных колебаний и управления этими колебаниями в целях синхронизации и придания им определенных параметров. Показано, что объединение фазовых систем в ансамбль предоставляет широкие способности для генерации хаотически модулированных колебаний и управления качествами таких колебаний.
Приобретенные результаты по генерации, синхронизации хаотически модулированных колебаний в ансамблях связанных фазовых систем, также по компьютерному моделированию процессов передачи информация с внедрением хаотических колебаний, свидетельствуют, что рассмотренные ансамбли позволяют удачно решать разные задачки, к примеру, построения новых коммуникационных систем с внедрением динамического хаоса для секретной передачи информация.