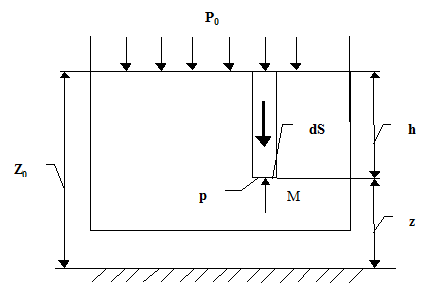
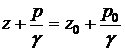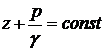Рассмотрим тот основной случай равновесия жидкости, когда на нее действует лишь одна массовая сила – сила тяжести. Свободная поверхность жидкости в этом случае, как известно, является горизонтальной плоскостью. Пусть жидкость содержится в сосуде (рис. 2.2) и на ее свободную поверхность действует давление p₀. Найдем величину гидростатического давления p в произвольно взятой точке M, расположенной на глубине h.

Рис. 2.2

Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т. е. вверх. Запишем сумму всех сил, действующих на рассматриваемый объем в вертикальном направлении:

где последний член представляет собой вес жидкости в указанном объеме. Силы давления по боковой поверхности цилиндра в уравнение не войдут, так как они нормальны к этой поверхности.

Сократив на dS и перегруппировав члены, получим (2.1):

Полученное уравнение называют основным уравнением гидростатики; оно позволяет определить давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления p₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости. Величина p₀ является одинаковой для всех точек объема жидкости, поэтому, учитывая второе свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково (закон Паскаля).

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня. Возьмем на произвольной высоте горизонтальную плоскость сравнения, от которой вертикально вверх будем отсчитывать координаты z. Обозначим через z координату точки M, через z₀ – координату свободной поверхности жидкости и заменив в уравнении (2.1) h на z₀ – z, получим (2.2):

Но так как точка M взята произвольно, то можно утверждать, что для всего рассматриваемого неподвижного объема жидкости:

Координата z называется нивелирной высотой. Величина  имеет также линейную размерность и называется пьезометрической высотой. Сумма  называется гидростатическим напором. Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости.