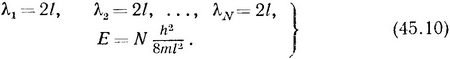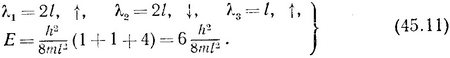В качестве наглядного примера рассмотрим систему из N квантовых частиц, заключенных в одномерном сосуде длиной l. Если обобщить этот случай на трехмерный сосуд — куб, то можно получить простую модель поведения электронов в металлах, которая по крайней мере качественно описывает большинство свойств обычных металлов: их реакцию на внешние электрическое и магнитное поля, их удельные теплоемкости и т. д.
Как мы уже установили ранее, волновыми функциями квантовой частицы, заключенной в одномерном сосуде, являются стоячие волны де Бройля с длинами волн:
а энергия этом частицы:
В случае одной частицы наинизшее состояние системы характеризуется значением n=1 (фиг. 183):
Если в сосуде находится несколько невзаимодействующих друг с другом частиц (между частицами не действуют силы), то полную волновую функцию системы можно сконструировать, приписывая каждой частице одну из упомянутых выше стоячих волн де Бройля.
Представим теперь, что в сосуде заключены две квантовые частицы. Если эти частицы бозоны, то наинизшему состоянию системы будет соответствовать случай, когда обе частицы описываются стоячей волной де Бройля с длиной волны 2l (фиг. 184):
Если же они фермионы, то, согласно принципу запрета, они не могут характеризоваться одинаковыми квантовыми числами1).
Поэтому, если частицы описываются одинаковыми волнами де Бройля, их спины должны быть направлены в противоположные стороны (фиг. 185):
При добавлении третьего, четвертого или N-ro бозона увеличивается лишь число частиц, находящихся в наинизшем состоянии, которое описывается волной де Бройля с длиной волны 2l (фиг. 186):
1) Волновые функции не могут быть антисимметричными, если их квантовые числа совпадают.
(Именно благодаря этому свойству бозонов с их помощью можно построить классическую волну. Чем большее число бозонов описывается одной и той же волновой функцией, тем больше становится вероятность их нахождения в заданном квантовом состоянии, что придает системе свойство классического непрерывного поля, например, электромагнитного.)
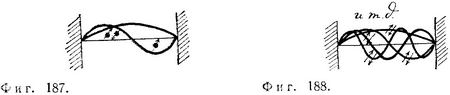
Если же к двум фермионам добавляется третий, четвертый или N-й фермион, то наблюдается совсем иная картина. Третий фермион не может быть описан волной де Бройля с длиной волны λ=2l, так как в этом случае, в какую сторону пи был бы направлен его спин, характеризующие его квантовые числа совпадали бы с квантовыми числами какой-либо из двух начальных частиц, — а это невозможно на основании принципа запрета. Поэтому для описания третьего фермиона следует выбрать следующую волну де Бройля. В результате основное состояние системы из трех фермионов характеризуется следующими параметрами (фиг. 187):
В случае N фермионов2) (фиг. 188):
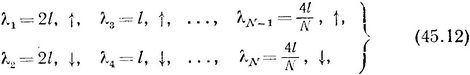
а энергия системы:
Таким образом, влияние принципа запрета на волновую функцию системы из большого числа фермионов сказывается в том, что фермионы не могут все-находиться в наинизшем квантовом состоянии (фиг. 189). Наинизшая энергия этой системы значительно превышает соответствующую энергию системы из такого же числа бозонов.
В результате энергия основного состояния электронов в металле оказывается чрезвычайно большой величиной, и для дальнейших взаимодействий остаются свободными лишь такие уровни, которые располагаются выше последнего занятого.
2) Для простоты положим, что N — четное число.
Волновая функция системы взаимодействующих частиц отличается от рассмотренной выше волновой функции из-за наличия сил, действующих между частицами. Однако, как мы убедимся при обсуждении периодической таблицы элементов, многие ее качественные свойства остаются прежними.