Пусть имеется конечный автомат, данный таблицей:

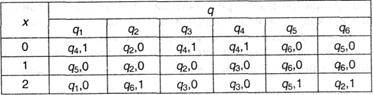
На базе ее составим другую таблицу, клеточки которой будут соответствовать всем разным парам q_iq_j (i ≠ j), заполнив ее согласно последующим правилам:

• если два состояния q_i и q_j неэквивалентны (т.е. для какого-нибудь значения входного знака х значения на выходе различаются), то соответственная клеточка зачеркивается;
• если в состояниях q_i и q_j для каждого х значения на выходе схожи, то в клеточки записываются все пары состояний q_vq_w (v ≠ w), хорошие от q_iq_j, в которые автомат может перейти из q_i и q_j при подаче 1-го и такого же входного знака.

Согласно первому правилу зачеркнутой оказалась, к примеру, клеточка, соответственная паре q₁q₂, так как при х = 0 на выходе выдаются различные значения (1 и 0). По второму правилу, к примеру для пары q₅q₆ следует записать пару q₂q₅ из последующих суждений: у q₅ и q₆ все выходные знаки схожи при схожих входных; х = 0 приводит к начальной паре q₅q₆; х = 1 приводит к паре схожих состояний q₆q₆.

Схожим образом анализируются другие сочетания.

В конце концов, следующими преобразованиями вычеркиваются клеточки, в каких находятся пары, надлежащие уже зачеркнутым ранее клеточкам. К примеру, следует зачеркнуть клеточку для пары q₁q₄, так как в ней содержится q₃q₆, также q₃q₄, потому что в ней есть q₂q₃. Потом опять необходимо зачеркнуть все клеточки, которые содержат пары, надлежащие вычеркнутым клеточкам. Процедура должна длиться до того времени, пока не сформируется таблица, в какой нельзя вычеркнуть ни одной из оставшихся клеток. Для рассматриваемого примера эти клеточки выделены жирной рамкой. Можно обосновать, что оставшиеся не вычеркнутыми клеточки соответствуют всем парам эквивалентных состояний. Это q₁q₃, q₂q₅, q₂q₆ и q₅q₆. Классы эквивалентности образуются состояниями, которые попарно эквивалентны. В данном случае это {q₁,q₃} и {q₂, q₅, q₆}. Состояния, не вошедшие в эти классы, эквивалентны только для себя и образуют собственные классы эквивалентности; в рассматриваемом примере это {q₄}. Таким образом, классы эквивалентности оказались выделенными.

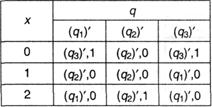
После выделения классов эквивалентности состояний для автомата М можно выстроить эквивалентный ему автомат M‘. В качестве входного и выходного алфавитов для М‘ возьмем надлежащие алфавиты М, а каждому классу эквивалентных состояний М сравним одно состояние М’. Для рассмотренного выше примера можно принять (q₁)’ ↔ {q₁, q₃}, (q₂)’ ↔ {q₂, q₅, q₆}, (q₃)‘ ↔ {q₄}.

Совсем получаем таблицу нового автомата М’.

Можно обосновать последующую аксиому*:

* Интересующихся подтверждением можно адресовать к книжке Л.А. Шоломова [48, с.125-126].