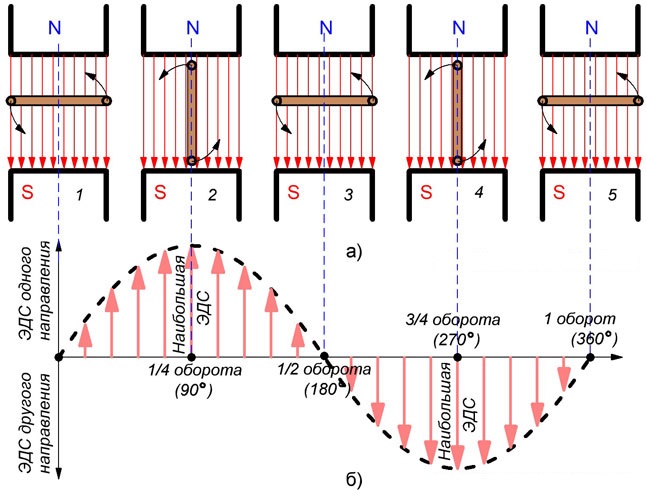
Возьмем проводник, согнутый в виде рамки и будем вращать его в равномерном магнитном поле (рисунок 1). При вращении рамки магнитный поток, охватываемый ею, будет изменяться, следовательно, в рамке возникнет ЭДС индук­ции.

Пусть рамка вращается с равномерной скоростью. Мы уже знаем, что величина ЭДС, индуктированной в рамке, будет тем больше, чем быстрее будет изменяться число маг­нитных силовых линий, охватываемых рамкой, или иначе, чем большее число магнитных силовых линий будут пересекать стороны рамки в единицу времени (например в одну секунду).

Примем за начальное то положение рамки, когда она охва­тывает наибольшее число магнитных силовых линий, т. е. когда плоскость ее перпендикулярна направлению магнитного потока. На рисунке 1 это положение отмечено цифрой 1.

Рисунок 1. Получение синусоидального переменного тока. а — ряд последовательных положений рамки в магнитном поле; б -график переменного тока (синусоида).

В начале вращения рамки ее стороны будут скользить почти вдоль магнитных силовых линий, пересекая очень малое число их, то есть магнитный поток, проходящий через рамку, будет изменяться очень медленно, следовательно, и наводимая этим изменением потока ЭДС индукции будет невелика.

По мере приближения рамки, к положению 2, когда плос­кость ее становится параллельной силовым линиям, количе­ство пересекаемых рамкой силовых линий возрастает (при по­стоянной скорости вращения рамки) а, следовательно, воз­растает и индуктируемая в ней ЭДС.

Когда рамка пройдет положение 2, действующая в рамке ЭДС начнет постепенно убывать и станет равной нулю, когда рамка сделает полуоборота (положение 3). Затем ЭДС будет снова возрастать, но уже в обратном направлении, так как теперь стороны рамки будут пересекать магнитные силовые ли­нии в противоположном направлении. В момент, когда рамка займет положение 4, т. е. сделает три четверти оборота, ЭДС будет наибольшей, после чего она начнет снова убывать и сде­лается равной нулю в тот момент, когда рамка завершит пол­ный оборот (положение 5).

При дальнейшем вращении рамки все явления будут по­вторяться в прежнем порядке. Так как ЭДС в рамке непре­рывно изменяется по величине и, кроме того, два раза в тече­ние каждого оборота изменяет свое направление, то и ток, вы­зываемый ею в рамке, будет также изменяться и по величине и по направлению.

Условимся изображать изменение переменной ЭДС, наво­димой в рамке при вращении ее в магнитном поле, таким об­разом, что по горизонтальной прямой линии (оси) слева направо будем откладывать в каком-нибудь масштабе угол поворота рамки или время, протекшее от начала поворота, а вверх и вниз (по вертикали) будем откладывать те ЭДС, которые наводятся в рамке при данном угле ее поворота. Вверх будем откладывать ЭДС одного направления, а вниз— ЭДС другого направления. В результате такого построения получим график изменения ЭДС в зависимости от угла по­ворота рамки или, что то же самое, в зависимости от времени, так как рамка вращается с постоянной скоростью. Кривая эта, изображенная на рисунке 1б, очень часто встречается в электро­технике и носит название синусоиды.

Итак, мы видим, что при равномерном вращении рамки в равномерном магнитном поле в ней индуктируется переменная ЭДС, изменяющаяся по периодическому закону, выражае­мому синусоидой; ЭДС и токи, изменяющиеся по такому за­кону, называются синусоидальными, а весь описанный процесс будет иметь название получение переменного синусоидального тока.

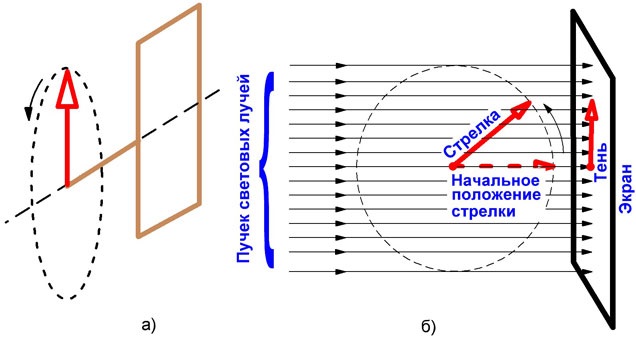
Свяжем мысленно с вращающейся рамкой стрелку, укреп­ленную на одной оси с рамкой (рисунок 2а). Направим на вра­щающуюся стрелку пучок параллельных световых лучей так, как это изображено на рисунке 2б, а с другой стороны стрелки поставим экран (например лист бумаги). Электродвижущая сила, индуктируемая в рамке, в каждый данный момент бу­дет пропорциональна длине тени, отбрасываемой стрелкой на экран. Длина тени в начальный момент, когда стрелка нахо­дится в горизонтальном положении, т. е. острием направлена в сторону экрана, будет равна нулю.

Рисунок 2. Модель синусоидального колебания. а -вместе с рамкой вращается стрелка; б -кончик тени от стрелки совершает синусоидальные колебания.

При вращении стрелки в направлении, указанном на рисунке, ее тень начнет удлиняться, вытягиваясь вверх. Сначала удлинение тени будет происходить быстро, но по мере при­ближения стрелки к вертикальному положению оно замедлит­ся и, наконец, совеем прекратится, когда длина тени сделается равной длине стрелки. После этого тень будет укорачиваться, сначала медленно, а затем все быстрее и быстрее и, наконец, сделается равной нулю в тот момент, когда стрелка, совершив полуоборота, займет горизонтальное положение. В то время, когда стрелка будет совершать следующую половину оборота, ее тень совершит такое же удлинение и укорочение, как и прежде, с той лишь разницей, что удлиняться она теперь будет не вверх, а вниз.

При каждом обороте стрелки ее тень будет совершать одно полное колебание.

Колебания тени вращающейся стрелки дают полную карти­ну изменения скорости движения электронов в проводнике при синусоидальном переменном токе. Скорость свободных элек­тронов в проводнике сначала невелика, затем электроны начи­нают двигаться все быстрее и быстрее (сила тока увеличивает­ся). В некоторый момент скорость электронов достигает своей максимальной величины (сила тока максимальна), после чего электроны постепенно замедляют свое движение и, наконец, совсем останавливаются (сила тока равна нулю).

Однако, практически электроны не делают остановки, так как они тотчас же начинают движение в обратном направле­нии (ток изменяет свое направление) с постепенно увеличи­вающейся скоростью (сила тока растет) и т. д.

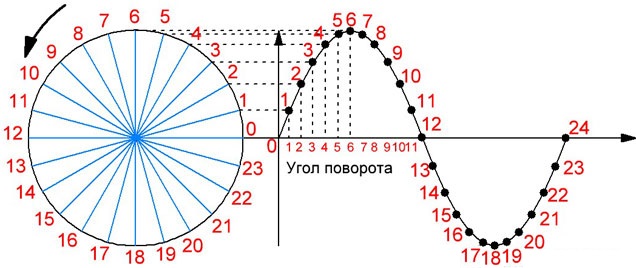
Начертим окружность, внутри которой наметим несколько положений радиуса, занимаемых им при равномерном движе­нии его конца по окружности. На рисунке 3 показано 24 после­довательных положения радиуса, занимаемых им через каж­дые 15° поворота. Справа от этой окружности проведем гори­зонтальную линию на высоте центра окружности. Разделим горизонтальную координатную ось также на 24 части, каждая из которых будет соответствовать 15° окружности.

Рисунок 3. Построение графика синусоидального переменного тока. Окружность и горизонтальная ось координат разделены на одинаковое число частей.

Из каждой отмеченной точки на горизонтальной оси прове­дем вертикальную линию, равную проекции радиуса на вертикальный диаметр или длине тени при данном угле поворо­та. Соединим плавной кривой концы всех вертикальных ли­ний. Эта кривая и будет синусоидой.

Вращающийся радиус, употребляемый при построении си­нусоиды, называется радиусом-вектором.