Интерференция составляет суть волновой теории. Линейная волна, набегающая на препятствие с двумя небольшими отверстиями, возбуждает волновую картину интерферирующих круговых волн, изученную ранее. На достаточном удалении от преграды положения минимумов (тех мест, где возмущение наиболее слабое) связаны с длиной падающей волны формулой:![]()
а положения максимумов (тех мест, где возмущение наиболее сильное, т. е. где гребни встречаются с гребнями или впадины со впадинами) определяются из выражения:
dsinθ = nλ. (18.2)
Таким образом, всего лишь полдлины волны определяет различие в положении максимумов и минимумов.
Юнг пишет:
«Если допустить, что свет любого заданного цвета состоит из колебаний определенной ширины, или определенной частоты, то окажется, что эти колебания ответственны за все те явления, которые мы раньше исследовали в случае волн на воде или звуковых импульсов. Было показано, что две одинаковые серии волн, исходящих из близко расположенных друг к другу центров, могут разрушить эффект каждой из них в определенных точках, а в других точках удвоить эти эффекты».
Но:
«Для того, чтобы две порции света вели себя подобным образом, они должны исходить из одного источника и приходить в одну и ту же точку по разным путям, причем эти пути не должны сильно отклоняться один от другого» (фиг. 255).
Иными словами, свет должен быть когерентным. Если гребни будут достигать обоих отверстий случайным образом, картина окажется смазанной. Там, где гребень мог бы встретиться со впадиной, с той же вероятностью гребень может встретиться с гребнем. Максимумы могут превратиться в минимумы. В результате вместо четкой картины мы увидим некую беспорядочную рябь.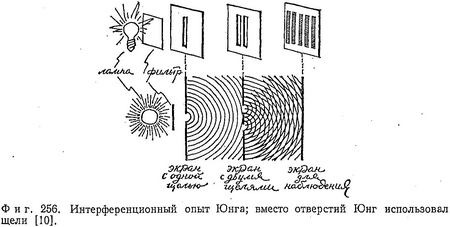
Проще всего добиться требуемой степени когерентности, если взять свет от одного источника, а затем расщепить его с помощью:
«дифракции, отражения, преломления или совместного действия этих эффектов… Но наиболее простой случай представляется, когда пучок однородного света падает на экран, имеющий два небольших отверстия или две щели (фиг. 256), которые можно рассматривать как центры расхождения, откуда свет дифрагирует по всем направлениям».
И далее:
«В этом случае, когда два вновь образованных пучка попадают на поверхность, поставленную на их пути, свет от них оказывается разделенным темными полосами на примерно равные части… В центре изображения всегда наблюдается светлая полоса, а другие светлые полосы по обе стороны от центра находятся на таких расстояниях, чтобы свет, идущий к ним из одной апертуры, проходил путь, больший, чем путь, проходимый светом из другой апертуры, на величину, равную ширине одной, двух, трех и более предполагаемых волн, для промежуточных же темных областей соответствующие различия в путях составляют половину, три вторых, пять вторых и более ширины предполагаемых волн».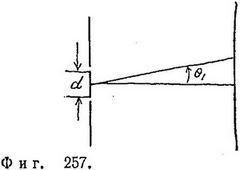
Если мы попытаемся объяснить наблюдаемую картину интерференцией волн (а чем же еще?), то, определяя положение темных полос, мы сможем узнать длину волны. Для этого надо измерить лишь расстояние между отверстиями d и угол θ1, под которым виден первый минимум (фиг. 257). Эти величины связаны между собой соотношением, полученным ранее:
dsinθ1 = λ/2 (18.3)
Измерив угол θ1, мы сразу же определяем длину волны излучения:
λ = 2dsinθ1. (18.4)
Конечно, это не лучший способ определения длины волны. На практике удобнее измерять расстояния между различными темными полосами; результат в этом случае окажется более точным. Но принцип остается прежним. Если мы наблюдаем именно свойства волн и если темные полосы возникают из-за интерференции волн, идущих через отверстия в преграде, то мы всегда сможем определить длину волны этих колебаний, зная d (расстояние между отверстиями) и синус угла между центральным максимумом и первым минимумом.
Из наблюдений известно, что расстояния между полосами в случаях красного и голубого цветов различны, а в случае белого света наблюдается смесь полос различных цветов. Можно предположить, что различие в цветах обусловлено различием в длинах волн, и поэтому расстояния до первой темной полосы для разных цветов не одинаковы. Именно к такому выводу и пришел Юнг:
«При сравнении результатов различных экспериментов мне удалось установить, что ширина предполагаемых колебаний, образующих чистый красный цвет, составляет в воздухе примерно одну тридцати шеститысячную дюйма, а ширина колебаний для чистого фиолетового цвета — примерно одну шестидесятитысячную… На основании этого можно показать, используя известное значение скорости света, что за одну секунду в наш глаз попадает около 500 миллионов наиболее медленных из таких колебаний».
В табл. 8 приведены длины волн некоторых известных цветов, полученных из опытных измерений дифракционных картин для этих цветов. Эти значения не являются точными, так как то, что мы воспринимаем как один цвет, состоит, как правило, из набора цветов в узком диапазоне длин волн. Нам только известно, что видимый спектр световых волн занимает интервал от 4*10-5 до 7,2*10-5 см, который соответствует чувствительности обычного человеческого глаза.