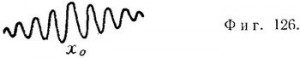Если вы любите парадоксы, то сейчас вы получите их в избытке. Интерпретация связанной с частицей волны как амплитуды вероятности приводит к результатам, кажущимся весьма необычными и странными, к результатам, которые поражают наш разум и смущают наши глаза и уши. Но не является ли наше изумление просто разочарованием в наших ожиданиях? А что представляют собой наши ожидания? Классическая теория движения, столь успешная при описании приливов и движений планет, оказывается абсолютно неверной, когда мы экстраполируем ее на область явлений, разыгрывающихся на расстояниях порядка 10-8 см и для масс порядка 10-27г. Здесь отчетливо проявляются волновые свойства частиц, и вероятностная интерпретация дает результаты, отличающиеся от тех, к которым мы привыкли в повседневной жизни.
Вероятно, самым удивительным и наиболее горячо обсуждаемым является вопрос об определенной ограниченности наших знаний в отношении тех вещей, которые с классической точки зрения всегда считались познаваемыми до конца.
Классическое описание движения содержит в себе скрытое предположение о том, что те элементарные корпускулы, из которых состоит наш мир, эти идеализированные бильярдные шары — твердые, массивные и неделимые (при этом нам совершенно безразлично, гладкие они или шершавые, окрашены они в желтый цвет или в голубой) — занимают определенное положение в пространстве. В любой момент времени можно сказать, где они находятся, с какой скоростью они движутся и какой путь прошли до этого. Основная задача классической физики и состоит в определении траектории частицы при известной системе сил, приложенных к ней (фиг. 118).
Классическая частица с массой m, на которую не действуют силы, движущаяся со скоростью v и заключенная между двумя стенками, продолжает в соответствии с законом инерции двигаться равномерно по прямой линии до соударения со стенкой. После соударения со стенкой она отражается (упруго) и движется в обратном направлении с тон же скоростью; положение частицы можно всегда определить (фиг. 119).
В квантовой механике та же частица с массой т, если мы считаем ее скорость заданной, связана с периодической волной, максимумы которой расположены на расстоянии:
λ = h/mv (41.1)
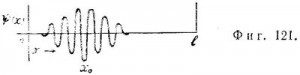
друг от друга и повторяются несколько раз вдоль прямой линии, соединяющей одну стенку сосуда с другой (фиг. 120). Если теперь спросить, где же находится квантовая частица, то мы получим следующий ответ: вероятность ее нахождения в какой-то точке между стенками определяется квадратом волновой функции. В примере, изображенном на фиг. 120, вероятность имеет максимальные и минимальные значения, периодически повторяющиеся от одной стенки к другой. Вряд ли мы можем теперь утверждать, что частица находится в точке х0 в момент t0 или в точке x1 в момент t1 и т. д. Характер волновой функции частицы, обладающей заданным импульсом, таков, что эта частица может в любой момент времени находиться с равной вероятностью в нескольких точках пространства. Можно утверждать, что импульс частицы равен mv, но говорить, что она действительно движется от одной точки к другой, уже нельзя. Такая ситуация выглядит довольно странной с классической точки зрения. Если отвлечься от твердости и. массивности бильярдного шара, то, пожалуй, единственное, что абсолютно очевидно при игре в бильярд, состоит в том, что в любой момент времени бильярдный шар находится в определенном месте на столе. Мы видим это собственными глазами, поражаясь иногда той траектории, которую описывает шар после удара искусного игрока.
Приведенный пример вовсе не означает, что квантовая частица вообще не может быть локализованной в некотором объеме (это утверждение может показаться еще более странным, чем предыдущее). Частица может считаться локализованной, если связанная с иен пол новая функция локализована в некотором объеме, как, например, на фиг. 121 или 122.
Импульс этой квантовой частицы, локализованной в окрестности точки x0 можно определить с помощью формулы де Бройля:
p = h/λ (41.2)
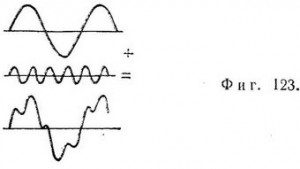
Но чему равна длина волны такой волновой функции? Ясно, что она не может характеризоваться какой-то одной длиной волны. Единственной волновой функцией, обладающей одной длиной волны, является периодическая функция, повторяющаяся вдоль линии, соединяющей стенки сосуда. Волновые же функции, изображенные на фиг. 121 и 122, можно представить в виде суммы большого числа периодических волновых функций с различными длинами волн. Поэтому, чтобы найти импульсы таких частиц, следует разложить соответствующие локализованные волновые функции на различные периодические функции, из которых эти локализованные функции состоят.
На вопрос, какие импульсы или какие длины волн следует приписать электрону (или кванту), если его положение строго локализовано в точке х0, следует ответить, что его волновая функция представляет собой сумму волн со всевозможными длинами. Таким образом, волновая функция, соответствующая локализованной в точке частице, состоит из суммы периодических волн, содержащей все волны — от самых длинных до самых коротких. С точки зрения квантовой механики это означает, что импульс частицы, локализованной в точке, может принимать с равной вероятностью любые значения от нуля до бесконечности.
Металлический шарик (классическая частица) может быть локализован в углублении на столе, так что он будет находиться в покое (фиг. 124). Таким образом, скорость шарика равна нулю, а его положение в пространстве точно известно. Квантовую частицу тоже можно локализовать вблизи точки х0, однако со временем она не будет оставаться локализованной, так как волновая функция, локализованная в какой-то момент времени t0 в точке х0 (фиг. 125), начинает расплываться (скорость расплывания зависит, помимо других факторов, от массы частицы), и через некоторый (небольшой) промежуток времен она перестает быть локализованной (фиг. 126). Это расплывание никак не соотносится с движением частицы в классическом смысле (частица для этого не только должна быть локализованной в какой-то точке, но и должна двигаться в определенном направлении с определенной скоростью). Расплывание связано с тем, что сам вакуум является для частиц диспергирующей средой — волны с различными длинами воли распространяются с разными скоростями, так как скорость кванта зависит от длины волны:
λ = h/mv (41.1)
Наиболее удивительный вывод, вытекающий из квантовой теории, состоит в том, что квантовая частица, хотя и обладает корпускулярным свойством дискретности, теряет тем не менее присущую классической частице способность одновременно занимать определенное положение в пространстве и иметь при этом определенную скорость.
Иногда эту мысль выражают следующим образом: невозможно одновременно измерить положение и скорость квантовой частицы. Позднее мы убедимся, что это действительно так. Но невозможность таких измерений не является, вообще говоря, достаточным основанием отрицать, что частица может одновременно обладать определенным положением и скоростью, или, выражаясь более точно, что следовало бы отказаться от попыток создать теорию, в которой квантовая частица одновременно имела бы определенные положение и скорость.
Проблема гораздо сложнее. Как мы уже видели, паша интерпретация волновой функции не позволяет приписывать ей, в классическом смысле, одновременных значений положения и импульса частицы. Если мы пытаемся записать волновую функцию при заданном значении импульса, то частица, с которой связана эта волновая функция, не занимает определенного положения в пространстве. Если же мы пытаемся записать функцию с учетом заданного положения в пространстве, то соответствующая частица не имеет определенного импульса. Таким образом, объекту, который с квантовой точки зрения содержит всю возможную информацию, нельзя одновременно приписать эти два классических свойства.