«В природе все должно быть гармонично и совершенно. Земля должна быть тоже совершенна. Но совершеннейшим из геометрических тел является шар. Значит, Земля – шар». Это первая зафиксированная гипотеза шарообразности Земли, была высказана известным древнегреческим ученым Пифагором (580 – 500 гг.). Сомнительная даже с точки зрения логики гипотеза оказалась во многом правильной.
Шарообразность Земли была установлена, как отмечалось выше, Эратосфеном примерно 2230 лет назад, однако такие же предположения были и у халдейских жрецов, изучавших движение Луны, Солнца, звезд и планет солнечной системы.
С открытием Д.Кассилем (1625 – 1712 гг.) полярного сжатия Юпитера и доказательствами И.Ньютона (1642 – 1727 гг.) о форме вращающегося в пространстве жидкого тела (форма сфероида или эллипсоида вращения) началось детальное изучение формы Земли.
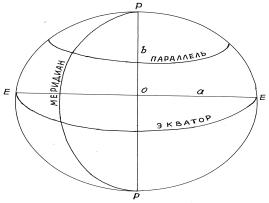
Очевидно, что шар и сфероид представляют собой математические фигуры с гладкими кривыми поверхностями (рис. 1.4), форма и размеры которых однозначно определяются по их основным параметрам: для шара — это радиус R, для сферооида — это размер одной из его полуосей (большой α или малой b) и полярное сжатие α, определяемое, как отношение (α — b)/α.
Рис. 1.4. Сфероид
В действительности физическая поверхность Земли имеет весьма сложную форму, которую невозможно описать простыми математическими зависимостями. Под физической поверхностью Земли понимается поверхность суши и невозмущенная поверхность всех внешних морей и океанов. Известно, что распределение масс (плотностей) в теле Земли весьма неравномерно. Это приводит к тому, что направления отвесных линий, если форму Земли в первом приближении принять за сфероид, не будут совпадать с направлениями нормалей к поверхности сфероида.
В результате образуется поверхность весьма сложной формы (уровенная поверхность), в каждой точке которой линия направления силы тяжести совпадает с нормалью к этой же поверхности. По предложению в 1873 г. немецкого физика Листинга (1808 – 1882 гг.) тело, ограниченное такой поверхностью, названо геоидом (землеподобным).
Геоид близок к сфероиду, но в общем случае не совпадает с ним. Отступления поверхности геоида от поверхности сфероида в некоторых местах Земли достигают ±(100 – 150) м. На акватории мирового океана форма геоида с помощью спутниковых наблюдений определяется весьма точно, с погрешностями порядка 0,1 – 0,3 м. На суше погрешность определения формы геоида уже значительна, порядка 1,5 – 2,0 м. В связи с этим для суши принята вспомогательная поверхность, положение которой определяется весьма точно. Эта поверхность называется поверхностью квазигеоида, а тело, ограниченное этой поверхностью, называют квазигеоидом.
Таким образом, зная форму геоида (квазигеоида), можно подобрать форму Земли (общий земной эллипсоид – ОЗЭ), определяемую простыми для использования математическими зависимостями, для которой выполнялись бы следующие условия:
- центр ОЗЭ совпадает с центром масс Земли;
- малая полуось совпадает с осью вращения Земли;
- объем ОЗЭ равен объему геоида (квазигеоида);
- сумма квадратов отклонений поверхности ОЗЭ от поверхности геоида (квазигеоида) в целом для всей Земли должна быть минимальной.
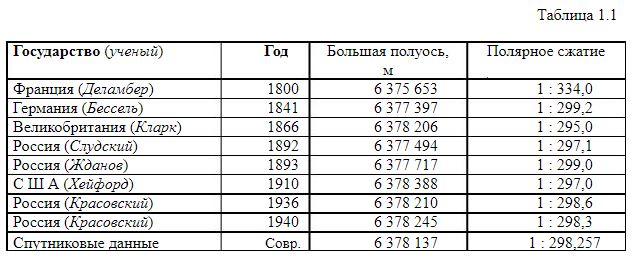
Для практических целей физическую поверхность Земли проектируют на вспомогательную поверхность, имеющую простую форму. Эта поверхность называется поверхностью относимости. Поверхность относимости должна незначительно отличаться от поверхности квазигеоида в пределах какойлибо территории, например, Европы, Азии, либо отдельного государства. В масштабах всей Земли удобно использовать общий земной эллипсоид, а в масштабах ограниченной территории за поверхность относимости удобно принимать другой эллипсоид (референц-эллипсоид), ориентировка которого в теле Земли может отличаться от ориентировки ОЗЭ, при этом малая ось референц-эллипсоида может и не совпадать с осью вращения Земли, а быть ей параллельной. В табл. 1.1 приведена историческая справка по определению параметров земного эллипсоида (референц-эллипсоидов).
До настоящего времени используются различные референц-эллипсоиды: в Германии – эллипсоид Бесселя (1841 г.), в Великобритании – эллипсоид Кларка (1880 г.), в США – эллипсоид Хейфорда (1909 г.). В России до 1942 г. использовался эллипсоид Бесселя. При детальном исследовании этого референц-эллипсоида оказалось, что он дает весьма большие погрешности в положении точек на поверхности Земли в пределах России. Под руководством русского ученого Ф.Н.Красовского (1878 – 1948 гг.) выполнены расчеты по определению параметров референц-эллипсоида для России. С 1946 г. параметры полученного референц-эллипсоида приняты для использования в геодезических расчетах: большая полуось α = 6378245 м, полярное сжатие α = 1 : 298,3. При этом следует отметить, что полученный референцэллипсоид (референц-эллипсоид Красовского) в наибольшей степени определяет параметры общего земного эллипсоида. Это подтверждают и современные спутниковые измерения.