При распространении электромагнитных волн в каждой точке пространства происходят периодически повторяющиеся изменения электрического и магнитного полей. Эти изменения можно представить в виде колебаний векторов напряженностей Н и Е в каждой точке пространства.

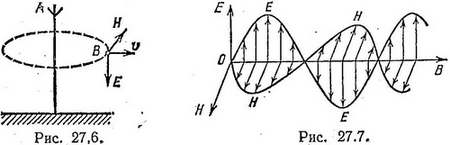
Максвелл показал, что колебания этих векторов в каждой точке электромагнитной волны происходят в одинаковых фазах и по двум взаимно перпендикулярным направлениям (рис. 27.6), которые в свою очередь перпендикулярны к вектору скорости распространения волны v.

Относительные расположения этих векторов в волне, распространяющейся от антенны А, показаны для примера в точке В. Взаимные расположения этих трех векторов в любой точке бегущей электромагнитной волны связаны правилом правого винта: если головку винта расположить в плоскости векторов Е и Н и поворачивать ее в направлении от Е к Н (по кратчайшему пути), то поступательное движение винта укажет направление вектора v, т. е. направление распространения самой волны и переносимой ею энергии.

Итак, векторы Е и Н колеблются в плоскости, перпендикулярной к вектору v. Это означает, что электромагнитные волны являются поперечными волнами. Расположение векторов Е и Н в различных точках волны для одного и того же момента времени показано на рис. 27.7.

Скорость распространения электромагнитных волн зависит от электрических и магнитных свойств среда, и, как вытекает из теории Максвелла, ее числовое значение выражается формулой:

v = 1/√(μ_cɛ_c) (27.6)

Поскольку μ_c=μμ₀ и ɛ_c=ɛɛ₀ то имеем:

v = 1/(√μɛ √μ₀ɛ₀) (27.7)

Так как для вакуума значения μ и ɛ равны единице, скорость распространения электромагнитных волн в вакууме:

с = 1/√ɛ₀μ₀ (27.8)

(Покажите, что из (27.8) для c получается значение, близкое 3*10⁸ м/с).

Из сравнения формул (27.8) и (27.7) получаем:

v = c/√μɛ, или c/v = √μɛ (27.9)

Величину n, показывающую, во сколько раз скорость распространения электромагнитных волн в вакууме больше, чем в какой-либо среде, называют абсолютным показателем преломления этой среды:

n = c/v (27.10)

Явление преломления волн и происхождение названия для n. Таким образом,

n = √μɛ (27.11)

Заметим, что диэлектрическая проницаемость среды ɛ в формуле (27.11) не совпадает с диэлектрической проницаемостью той же среды ɛ_ст, рассмотренной в электростатике, так как ɛ зависит от частоты колебаний. Поэтому при расчетах по формулам (27.6), (27.7), (27.9), (27.11) нельзя брать значения ɛ из таблиц, приводимых в электростатике. Однако ɛ всегда больше единицы, а μ для диэлектриков, в которых могут распространяться электромагнитные волны, практически можно считать равным единице. Следовательно, в любой среде скорость распространения электромагнитных волн меньше, чем в вакууме, т. е.  всегда больше единицы.

Для электромагнитных волн справедлива формула (24.23): v = λv. Для вакуума эта формула принимает вид:

c = λ₀v, (27.12)

где λ₀ — длина волны в вакууме.

Напомним, что при переходе волн из одной среды в другую частота колебаний остается неизменной, а длина волны изменяется. Следует иметь в виду, что длину электромагнитной волны всегда указывают для вакуума, если нет специальных оговорок. На практике в основном используют волны с высокой частотой колебаний, так как энергия, переносимая волнами, пропорциональна квадрату частоты. Кроме того, чем выше частота колебаний, тем легче осуществить направленное излучение электромагнитных волн.

Электромагнитные волны имеют большое значение и при передаче электрической энергии по проводам, которые для волн являются как бы направляющими рельсами. Электрические сигналы вдоль проводов распространяются со скоростью 3*10⁸ м/с т. е. при замыкании цепи ток возникает практически одновременно во всей цепи, в то время как скорость направленного движения электронов в проводе составляет десятые доли сантиметра в секунду.