Суперпозиция электростатических сил
Из закона Кулона и из соглашения, что электростатическое притяжение или отталкивание есть сила (поэтому ее можно описать вектором), вытекает правило о том, что нужно делать в случае трех или более зарядов. Допустим, требуется определить силу, которая действует на третий заряд со стороны двух других зарядов (фиг. 274).
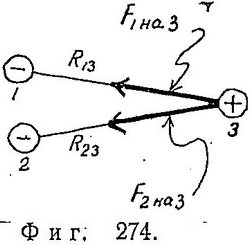
С помощью закона Кулона можно определить силы, с которыми первый и второй заряды действуют на третий (на фиг. 274 эти силы обозначены соответственно через F1 на 3 и F2 на 3). Полная сила, приложенная к третьему заряду, равна векторной сумме этих сил. В этом и состоит наиболее важное свойство электрических сил (гравитационных тоже), заключающееся в том, что сила взаимодействия двух зарядов не изменяется при наличии третьего, четвертого или пятого зарядов. Оно позволяет нам определять действие целой системы зарядов на любой другой заряд путем непосредственного сложения эффектов отдельных зарядов системы.
Пример. Какова сила взаимодействия двух зарядов в 5 эл. ст. ед. и 25 эл. ст. ед., расположенных на расстоянии 10 см друг от друга?![]()
Если оба заряда положительны, сила будет отталкивающей. То же самое можно сказать про два отрицательных заряда (отсюда видна условность названий «положительный» и «отрицательный»). Если же один заряд отрицателен, а другой положителен (например, — 5 эл. ст. ед. и 25 эл. ст. ед. или 5 эл. ст. ед. и—25 эл. ст. ед.), на каждый заряд будет действовать сила притяжения в 1,25 дин.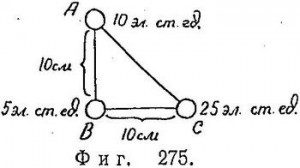
Допустим, мы внесли третий заряд, как показано на фиг. 275. Спрашивается: чему равны горизонтальная и вертикальная составляющие силы, действующие на заряд B?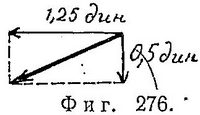
Заряд С оказывает действие (направленное влево) на заряд В. Заряд 10 эл. ст. ед. (А) также отталкивает заряд В, но эта сила направлена вниз. Ее величина:![]()
Следовательно, (фиг. 276):
Fгориз = 1.25 дин (направлена влево),
Fверт = 0.5 дин (направлена вниз). (19.8)
Введение электрического поля
Понятие поля, которое мы собираемся сейчас ввести, можно было определить и в случае гравитационных сил. Оно возникает при попытке описать силу, которая действует на заряд, находящийся в заданной точке пространства, со стороны многих других зарядов, и приписывает этой точке пространства определенное свойство, влияющее на движение частиц. Мы согласились, что сила, действующая на точечный заряд со стороны других зарядов, равна векторной сумме сил со стороны отдельных зарядов. В случае трех зарядов, рассмотренном выше, на третий заряд действует сила:
F3 = F1 на 3 + F2 на 3. (19.9)
Величина и знак силы F1 на 3 определяются по формуле:![]()
а величина и знак силы F2 на 3 — по формуле:
![]()
Каждое из этих выражений содержит множитель q3; это следует непосредственно из закона Кулона. Если бы было N зарядов, векторная сумма состояла бы из N слагаемых, все величины которых были бы пропорциональны заряду, находящемуся в точке 3.
Это дает возможность применить прием, кажущийся тривиальным, с тем чтобы прийти к понятию электрического поля. Мы выносим из выражения для силы множитель q3 и вводим новую величину Е:
F1 на 3 =q3E1 на 3 (19.12)
Эту величину, т. е. вектор E1 на 3, мы называем электрическим полем, которое возбуждает заряд 1 в точке 3. Отметим, что величина электрического поля не зависит от того, есть ли какой-нибудь заряд в точке 3. Далее, результирующее электрическое поле в точке 3 равно векторной сумме электрических полей, создаваемых каждым зарядом системы; на основании этого мы можем ввести полное электрическое поле в точке 3:
E3 = E1 на 3 + E2 на 3 + … + EN на 3 (19.13)
В системе СГС электрическое поле измеряется в дин/эл. ст. ед. заряда.
Не удивительно, если покажется непонятным, для чего понадобилось вводить дополнительную величину. Впервые ее ввел Фарадей для того, чтобы сделать более наглядным действие одних зарядов на другие. Максвелл пытался представлять электрическое поле как механическое натяжение в эфире. С тех пор значение электрического поля распространилось далеко за рамки любой механической интерпретации. Вместе с такими понятиями, как импульс или энергия, электрическое поле в конце концов стало играть более важную роль, чем частные теории, из которых родились эти понятия. В этом мы убедимся, когда будем изучать электромагнитное излучение.

Электрическое поле можно назвать векторной функцией. С каждой точкой пространства связан вектор, и этот вектор, умноженный на заряд, дает величину силы, которая действует на этот заряд в данной точке со стороны зарядов, создающих поле. Если нам известно электрическое поле во всех точках пространства, это означает, что нам известна сила, которая будет действовать на заряд в любой точке, даже если мы не знаем, какова та система зарядов, которая создала это поле1). В этом заключается главное удобство введенного понятия; в некоторых случаях бывает проще оперировать с существующим полем, чем с заряженными частицами, создающими его.
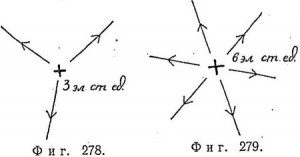
Электрическое поле сложно изобразить на рисунке, так как для этого в каждой точке пространства необходимо нарисовать вектор. Однако можно рисовать векторы лишь в некоторых точках пространства, как, например, на фиг. 277, где изображено электрическое поле положительного точечного заряда. Длины векторов уменьшаются с расстоянием как 1/r2, а направлены они все по радиусам от заряда. Иногда для наглядности рисуют не векторы, а сплошные линии, которые везде параллельны полю в тех точках, через которые эти линии проходят. При этом величина поля характеризуется густотой линий. Например, мы можем договориться, что из заряда в 1 эл. ст. ед. должна выходить одна линия. Тогда из заряда в 3 эл. ст. ед. будут выходить 3 силовые линии, а из заряда в 6 эл. ст. ед.— шесть линий, как показано на фиг. 278 и 279 (см. также фиг. 280).
1) При этом предполагается, что введение нового заряда не нарушает первоначальное распределение зарядов, для которого было найдено поле.
На фиг. 281 изображены силовые линии электрического поля двух разноименно заряженных пластин (такая система называется емкостью, или конденсатором). За исключением краев, плотность электрических силовых линий между пластинами постоянна. То же самое относится к величине и направлению соответствующего электрического поля.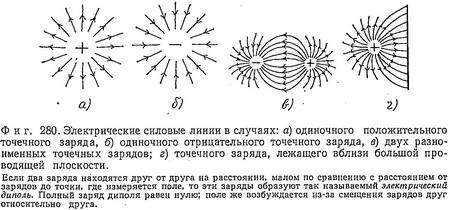
Иногда случается, что мелкие предметы выстраиваются параллельно электрическому полю, если создать необходимые условия. Как ни странно, но именно так ведут себя семена травы, взвешенные в непроводящей жидкости. (Почему так происходит?) Если создать в такой жидкости электрическое поле, погружая в Нее заряженные тела, семена выстроятся вдоль направления поля, и мы сможем наблюдать картину силовых линий, образованную этими семенами. Несмотря на внешнюю привлекательность таких картин, они довольно обманчивы, так как могут создать ошибочное впечатление, что силовые линии реально существуют.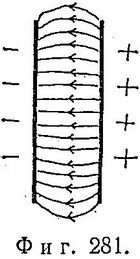
Подводя итоги сказанному, мы утверждаем, что электрическое поле есть векторная функция пространственных координат (каждой точке пространства соответствует вектор), определяемая распределением зарядов. Если в какой-либо точке пространства поместить заряд q, не нарушающий первоначальное распределение зарядов, то на этот заряд будет действовать сила:
F = qЕ. (19.14)
Таким образом, зная электрическое поле, мы в состоянии определить силу, приложенную к заряду в любой точке пространства, даже если нам неизвестно порождающее поле распределение зарядов (фиг. 282).

Спрашивается: каким образом можно найти электрическое поле, если задано определенное распределение зарядов? В простых случаях мы можем воспользоваться законом Кулона, а затем просуммировать вклады от всех зарядов. Для более сложных случаев, включающих произвольное распределение зарядов, разработаны весьма изящные методы. Исходя из закона Кулона, можно вывести несколько мощных теорем, позволяющих просто и быстро определять поля в случае относительно сложных, но симметричных распределений зарядов. Однако нас не интересуют эти методы, поэтому мы не будем их здесь описывать.