Рассмотрим частицу массы m, имеющую положительный заряд q и движущуюся в однородном магнитном поле В. Под однородным магнитным полем мы понимаем поле, величина и направление которого постоянны во всем объеме, в котором движется частица. Мы ввели одно неявное упрощение. Нас не интересует вопрос, какое распределение токов вызывает заданное распределение поля. (Практически однородное поле может быть получено внутри соленоида.) Мы просто полагаем, что с помощью какой-то токовой системы нам удалось создать такое поле. В этом состоит одно из упрощений, обусловленных введением понятия поля. В результате все расчеты четко разделяются на два этапа.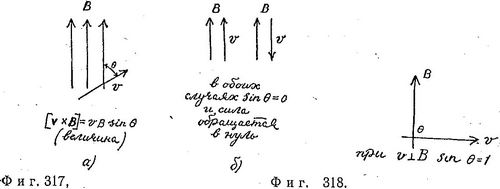
На первом этапе вычисляется поле по заданному распределению токов.
На втором этапе рассчитывается сила, а затем движение частицы, исходя из заданного распределения поля. Мы предполагаем, что каким-то образом нам удалось в некоторой области пространства создать однородное магнитное поле. Далее мы предполагаем, что в этой области электрическое поле отсутствует (вблизи нет не скомпенсированных зарядов). Тогда сила, испытываемая заряженной частицей в таком однородном магнитном поле, определяется вторым членом в формуле Лоренца:![]()
Величина вектора [v x В] в случае, когда v не перпендикулярен В, равна vBsinθ, где θ — угол между векторами v и В (фиг. 317, а).
Сила Лоренца обращается в нуль, если синус угла между скоростью частицы и магнитным полем равен нулю. Это происходит, когда частица движется параллельно или антипараллельно направлению поля (фиг. 317, б). Если скорость и магнитное поле заданы, то сила максимальна, когда sinθ = 1, т. е. когда v перпендикулен В, как на фиг. 318; в этом случае:![]()
Рассматривая частный случай, когда заряженная частица движется перпендикулярно направлению поля (фиг. 319), мы по существу ничего не теряем, но зато все наши вычисления упрощаются. В этом случае величина силы, действующей на движущуюся в магнитном поле положительно заряженную частицу1), равна:
а направлена она всегда перпендикулярно скорости, как на фиг. 319. Не проводя никаких вычислений, мы можем сразу же сделать несколько важных качественных выводов, касающихся действия такой силы на заряженную частицу.
1) Если частица заряжена отрицательно, величина силы остается такой же, а ее направление изменяется на противоположное.
Сначала рассмотрим следствие из того утверждения, которое мы повторили несколько раз: сила всегда остается перпендикулярной скорости, даже если скорость непрерывно изменяет свое направление. Из определения работы следует, что такая сила не совершает над частицей работы, поэтому кинетическая энергия частицы сохраняется. А, следовательно, мы можем заключить, что в отсутствие других сил скорость частицы, движущейся в магнитном поле, не изменяется. Удивительно, но факт! Тем не менее сила действует и вызывает ускорение тела. Это ускорение изменяет направление движения заряженной частицы, но не ее скорость. При таких условиях заряженная частица будет двигаться по окружности. Мы знаем, что при движении частицы по окружности ее ускорение записывается особенно просто: α=v2/R. В результате получим:
F = ma,
Отсюда видно, что, зная величину магнитного поля (его можно либо вычислить по известному распределению внешнего тока, возбуждающего поле, либо измерить с помощью различных приборов, причем, как правило, для его определения используют оба эти метода), заряд летящей частицы и радиус ее траектории, можно определить ее массу.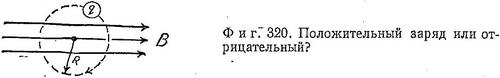
Пример. Частица движется по окружности радиусом R=5,65 см в однородном магнитном поле B=10 Гс со скоростью ν=109 см/с (фиг. 320). Чему равно отношение заряда частицы к ее массе, q/m?
Это число представляет определенный интерес, так как оно характеризует отношение заряда к массе в случае электрона (как мы увидим позже, это отношение впервые нашел Дж. Дж. Томсон).
НВидимый след образован пузырьками, возникающими в жидком водороде при прохождении заряженной частицы. Если бы заряд частицы изменил знак, а все остальное осталось бы прежним, частица начала бы «раскручиваться» в другую сторону, так как сила изменила бы свое направление. Такие траектории (треки) постоянно наблюдаются на фотографиях, полученных в пузырьковых камерах или камерах Вильсона при изучении элементарных частиц.

