Нуклоны в атомном ядре связаны между собой ядерными силами; поэтому чтобы разделить ядро на составляющие его отдельные протоны и нейтроны, необходимо затратить большую энергию. Эта энергия называется энергией связи ядра.

Такая же по величине энергия освобождается, если свободные протоны и нейтроны соединяются и образуют ядро. Следовательно, согласно специальной теории относительности Эйнштейна масса атомного ядра должна быть меньше суммы масс свободных протонов и нейтронов, из которых оно образовалось. Эта разность масс Δm, соответствующая энергии связи ядра Eсв, определяется соотношением Эйнштейна:

Есв = с²Δm.     (37.1)

Энергия связи атомных ядер настолько велика, что эта разность масс вполне доступна непосредственному измерению. С помощью масс-спектрографов такая разность масс действительно обнаружена для всех атомных ядер.

Разность между суммой масс покоя свободных протонов и нейтронов, из которых образовано ядро, и массой ядра называется дефектом массы ядра. Энергию связи обычно выражают в мегаэлектронвольтах (МэВ) (1 МэВ=10⁶ эВ). Поскольку атомная единица массы (а. е. м.) равна 1,66*10^-27 кг, можно определить соответствующую ей энергию:

Е = mс², E а.е.м = 1.66*10^-27*9*10¹⁶ Дж,

или

E а.е.м = (1.66*10^-27*9*10¹⁶ Дж)/(1,6*10^-13 Дж/МэВ) = 931,4 МэВ.

Энергию связи можно измерять непосредственно по балансу энергии в реакции расщепления ядра. Так впервые была определена энергия связи дейтрона при его расщеплении γ-квантами. Однако из формулы (37.1) энергию связи можно определить гораздо точнее, поскольку с помощью масс-спектрографа можно измерить массы изотопов с точностью 10^-4%.

Подсчитаем, например, энергию связи ядра гелия ⁴₂Не (α-частицы). Его масса в атомных единицах равна М (⁴₂Не) =4,001523; масса протона mр=1,007276, масса нейтрона mn=1,008665. Отсюда дефект массы ядра гелия

Δm = 2/mp + 2mn — М (⁴₂Не),

Δm = 2*1,007276 + 2*1,008665—4,001523 = 0,030359.

Умножив на E а.е.м = 931,4 МэВ, получим

Есв = 0,030359*931,4 МэВ ≈ 28,3 МэВ.

С помощью масс-спектрографа были измерены массы всех изотопов и определены значения дефекта массы и энергии связи ядер. Значения энергии связи ядер некоторых изотопов приведены в табл. 37.1. С помощью таких таблиц выполняют энергетические расчеты ядерных реакций.

Если суммарная масса ядер и частиц, образовавшихся в какой-либо ядерной реакции, меньше суммарной массы исходных ядер и частиц, то в такой реакции освобождается энергия, соответствующая этому уменьшению массы. Когда общее число протонов и общее число нейтронов сохраняется, уменьшение суммарной массы означает, что в результате реакции увеличивается общий дефект массы и в новых ядрах нуклоны еще сильнее связаны друг с другом, чем в исходных ядрах. Освобождающаяся энергия равна разности между суммарной энергией связи образовавшихся ядер и суммарной энергией связи исходных ядер, и ее можно найти с помощью таблицы, не вычисляя изменение общей массы. Эта энергия может выделяться в окружающую среду в виде кинетической энергии ядер и частиц или в виде γ-квантов. Примером реакции, сопровождающейся выделением энергии, может служить любая самопроизвольная реакция.

Проведем энергетический расчет ядерной реакции превращения радия в радон:

²²⁶₈₈Ra → ²²²₈₆Rn + ⁴₂He.

Энергия связи исходного ядра составляет 1731,6 МэВ (табл. 37.1), а суммарная энергия связи образовавшихся ядер равна 1708,2 + 28,3 = 1736,5 МэВ и больше энергии связи исходного ядра на 4,9 МэВ.

Следовательно, в этой реакции освобождается энергия 4,9 МэВ, которая в основном составляет кинетическую энергию α-частицы.

Если в результате реакции образуются ядра и частицы, суммарная масса которых больше, чем у исходных ядер и частиц, то такая реакция может протекать только с поглощением энергии, соответствующей этому увеличению массы, и самопроизвольно никогда не произойдет. Величина поглощенной энергии равна разности между суммарной энергией связи исходных ядер и суммарной энергией связи образовавшихся в реакции ядер. Таким путем можно рассчитать, какой кинетической энергией должна обладать при столкновении с ядром-мишенью частица или другое ядро, чтобы осуществить такого рода реакцию, или вычислить необходимую величину γ-кванта для расщепления какого-либо ядра.

Так, минимальная величина γ-кванта, необходимая для расщепления дейтрона, равна энергии связи дейтрона 2,2 МэВ, поскольку в этой реакции:

²₁H + γ → ¹₁H + ₀n¹

образуются свободные протон и нейтрон (Есв = 0).

Хорошее совпадение подобного рода теоретических расчетов с результатами опытов показывает правильность приведенного выше объяснения дефекта массы атомных ядер и подтверждает установленный теорией относительности принцип, пропорциональности массы и энергии.

Следует заметить, что реакции, в которых происходит превращение элементарных частиц (например, β-распад), также сопровождаются выделением или поглощением энергии, соответствующей изменению общей массы частиц.

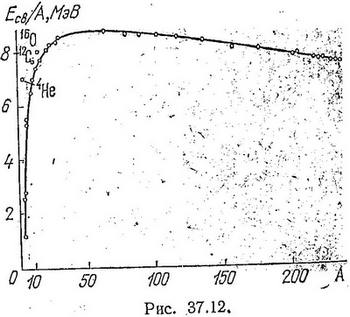
Важной характеристикой ядра служит средняя энергия связи ядра, приходящаяся на один нуклон, Eсв/A (табл. 37.1). Чем она больше, тем сильнее связаны между собой нуклоны, тем прочнее ядро. Из табл. 37.1 видно, что для большинства ядер величина Есв/А равна примерно 8 МэВ на нуклон и уменьшается для очень легких и тяжелых ядер. Среди легких ядер выделяется ядро гелия.

Зависимость величины Есв/А от массового числа ядра А показана на рис. 37.12. У легких ядер большая доля нуклонов находится на поверхности ядра, где они не полностью используют свои связи, и величина Есв/А невелика. По мере увеличения массы ядра отношение поверхности к объему уменьшается и уменьшается доля нуклонов, находящихся на поверхности. Поэтому Есв/А растет. Однако по мере увеличения числа нуклонов в ядре возрастают кулоновские силы отталкивания между протонами, ослабляющие связи в ядре, и величина Есв/А у тяжелых ядер уменьшается. Таким образом, величина Есв/А максимальна у ядер средней массы (при А = 50—60), следовательно, они отличаются наибольшей прочностью.

Отсюда следует важный вывод. В реакциях деления тяжелых ядер на два средних ядра, а также при синтезе среднего или легкого ядра из двух более легких ядер получаются ядра прочнее исходных (с большей величиной Есв/А). Значит, при таких реакциях освобождается энергия. На этом основано получение атомной энергии при делении тяжелых ядер и термоядерной энергии — при синтезе ядер.