Разглядим функцию f(x, y) = х — у, которая может быть получена при помощи оператора минимизации:
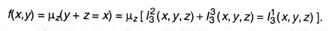
Вычислим, к примеру, f(7,2,), т.е. значение функции при у = 2 и х = 7. Положим у = 2, а х будем придавать поочередные значения:
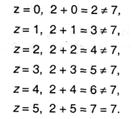
Таким образом, найдено значение функции f(7,2) = 5.
Введем определение:
Частичная функция f(х1,…,хп) именуется отчасти рекурсивной, если ее можно получить конечным числом операций суперпозиции, примитивной рекурсии и минимизации, исходя только из простых функций S1, 0n и Imn.
Класс отчасти рекурсивных функций обширнее класса примитивно рекурсивных функций, т.к. все примитивно рекурсивные функции являются везде определенными, а посреди отчасти рекурсивных функций встречаются функции не везде определенные, также нигде не определенные.
Понятие отчасти рекурсивной функции является одним из основных понятий теории алгоритмов. Значение его состоит в последующем. С одной стороны, любая стандартно данная отчасти рекурсивная функция вычислима методом некой процедуры механического нрава, отвечающей интуитивному представлению об методах. С другой стороны, какие бы классы точно очерченных алгоритмов ни строились, во всех случаях постоянно оказывалось, что вычислимые средством их числовые функции являлись отчасти рекурсивными. Потому принятой является научная догадка, формулируемая как тезис Черча.