Вещественное число X может быть представлено в 2-ух формах — естественной и нормализованной. В естественной форме у X имеется целая и дробная части, меж которыми помещается разделитель (запятая либо точка), к примеру 123,4567. Но такая запись неудобна для очень огромных либо, напротив, очень малых чисел. Не считая того, внедрение таковой формы (она именуется также «представление числа с фиксированной запятой») в компьютере вызвало бы понижение точности вычислений из-за необходимости приведения в соответствие разрядов обрабатываемых чисел и связанных с этим округлений либо могло бы породить ситуацию, именуемую переполнением, когда старший разряд числа не умещается в отведенной разрядной сетке. По обозначенным причинам вещественные числа в компьютере представляются в нормализованном виде (другое заглавие — «представление числа с плавающей запятой»), основным достоинством которой является автоматическое масштабирование числа на каждом шаге обработки, что, с одной стороны, обеспечивает очень вероятную точность вычислений, а с другой — устраняет от необходимости принимать конструктивные меры по предотвращению переполнения (кроме довольно экзотичных ситуаций с выходом числа за отведенную разрядную сетку). На самом деле, это универсальная форма записи всех чисел, не считая определенных как «тип: целые» (к примеру, Integer, Word либо Byte в PASCAL’e).

Поначалу познакомимся с необходимыми понятиями применительно к 10-ной системе счисления.

Число Х₁₀ именуется нормализованным, если оно представлено в виде Х₁₀ = ± M₁₀ ∙ 10^±k10.

В этой записи М₁₀ именуется мантиссой нормализованного числа; значения мантиссы лежат в интервале 0,1 ≤ М₁₀ ≤ 1. k₁₀ именуется порядком нормализованного числа — это целое положительное десятичное число. Примеры: -1234₁₀ = -0,1234∙10⁴; 0,03456₁₀ = 0,3456∙10^-1.

Понятие нормализованного числа следует отличать от понятия числа в обычной форме; данная форма довольно нередко применяется при записи чисел в арифметике, физике, технических дисциплинах и отличается от нормализованного представления тем, что мантисса лежит в интервале 1 ≤ M₁₀ < 10, к примеру, k_Б = 1,38∙10^-23.

При нормализации происходит расчленение «составляющих» числа с выделением знака числа, мантиссы, знака порядка и порядка — как будет показано ниже, это делает определенные удобства при хранении и обработке чисел в компьютере.

Аналогично нормализации десятичного числа можно в нормализованной форме представить и число в случайной системе счисления р:

При всем этом значения мантиссы лежат в интервале р^-1 ≤ М_р < 1 (т.е. 1-ая означающая цифра мантиссы всегда ненулевая), а показатель степени представляется в системе р (k_p). К примеру, для р = 2:

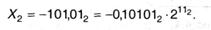
Мантисса размещается в промежутке 0,1₂ ≤ М₂ < 1, что соответствует десятичному интервалу 0,5₁₀ ≤ M₁₀ < 1.

Подобно задачке о преобразовании целых и дробных чисел, можно поставить задачку о преобразовании представления числа в нормализованной форме в системе счисления р к нормализованному представлению в системе q. Практическое значение такового преобразование заключается в том, что, как было сказано, в компьютере все вещественные числа хранятся и обрабатываются в нормализованном двоичном представлении и, как следует, при их вводе осуществляется перевод Х₁₀ → Х₂, а при выводе — оборотный перевод Х₂ → Х₁₀. Но до этого, чем дискуссировать таковой перевод, нужно разглядеть, как делается преобразование вещественного числа из естественной формы к нормализованному виду.

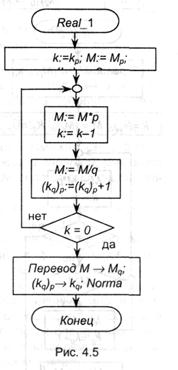
При нормализации различаются ситуации Х_р > 1 и Х_р < р^-1. В первом случае для нормализации нужно перемещать разделитель разрядов на лево по числу до того времени, пока не пропадет целая часть числа, но 1-ая цифра после разделителя будет ненулевой; каждое перемещение разделителя на 1 разряд на лево эквивалентно делению числа на р и, чтоб число не изменялось, показатель должен возрастать на единицу при каждом сдвиге. Если обозначить эту операцию N_← (будем именовать ее «нормализация влево»), то N_←[(123,45)₁₀] = 0,12345₁₀∙10³; N_←[(23,4∙10⁵)₁₀] = 0,234₁₀∙10⁷; N_←[(1212,2)₃] = 0,12122₃∙3¹¹. Аналогично можно ввести операцию «нормализация вправо» (N_→), обеспечивающая нормализацию чисел наименьших р^-1; разумеется, такие числа нужно множить на р с одновременным уменьшением показателя на 1 до того времени, пока 1-ая цифра после разделителя станет ненулевой. К примеру, N_→[(0,000101∙2^-101)₂] = 0,101∙2^-1000; N_→[(0,000987)₁₀] = 0,987₁₀∙10^-3. Общий метод нормализации можно изобразить в виде блок-«нормализация вправо» (N_→), обеспечивающая нормализацию чисел наименьших р^-1; разумеется, такие числа нужно множить на р с одновременным уменьшением показателя на 1 до того времени, пока 1-ая цифра после разделителя станет ненулевой. К примеру, N_→[(0,000101∙2^-101)₂] = 0,101∙2^-1000; N_→[(0,000987)₁₀] = 0,987₁₀∙10^-3. Общий метод нормализации можно изобразить в виде блок-схемы на рис. 4.4.

При практической реализации данного метода не стоит забывать, что изменение значения k_p на 1 должно выполняться по правилам математики системы счисления р. В предстоящем по мере надобности проведения нормализации в процессе каких-то преобразований будем просто ссылаться на приведенный метод как готовый модуль.

Вернемся к задачке перевода нормализованного числа из одной сиcтемы счисления в другую. Пусть, имеется число Х_р = ±М_р ∙ р^±kp для которого нужно отыскать соответственное ему X_q = ±M_q ∙ р^±kq . Представляется довольно естественным, что преобразование не затронет символов мантиссы и показателя степени. Таким образом, для воплощения преобразования нужно установить соответствие меж (М_р, k_p) и (M_q, k_q). Оно выходит довольно легко, исходя из того, что Х_р = X_q, откуда следует:

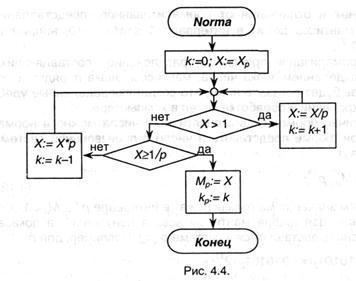
Из (4.13) вытекает, что для воплощения преобразования можно М_р помножить на р_kp , т.е. перейти к естественной форме числа в системе р, перевести его в систему q, а потом восстановить. Но в таком варианте действий пропадает точность числа и может быть переполнение на промежных шагах преобразования. Во избежание этого нужно чередовать умножение (либо деление) на р и нормализацию по основанию q. При всем этом, так как все операции производятся по правилам математики в системе р, будут получены не (M_q, k_q) в окончательном варианте, а их представления в системе р — обозначим их (M_q)_p и (k_q)_p, которые потом необходимо будет перевести в систему q. Различаются также ситуации k_p ≥ 0 и k_p < 0 — в первом случае нужно множить изначальное и промежные значения мантиссы на р и для нормализации разделять на q, во 2-м — напротив. Всякий раз при умножении либо делении на р показатель k_p будет поменять собственный значение на 1; продолжать деяния следует до того времени, пока не выполнится условие k_p = 0. Метод действий для ситуации k_p ≥ 0 представлен на рис.4.5.