Выполнить преобразование 12310 → Z5.
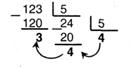
Остатки от деления (3, 4) и итог последнего целочисленного деления (4) образуют оборотный порядок цифр нового числа. Как следует, 12310 = 4435.
Нужно увидеть, что приобретенное число нельзя читать «четыреста 40 три», так как 10-ки, сотки, тысячи остальные подобные обозначения чисел относятся только к десятичной системе счисления. Прочитывать число следует обычным перечислением его цифр с указанием системы счисления («число четыре, четыре, три в пятиричной системе счисления»).
Метод 2 вытекает из соотношения (4.4); деяния выполняются в согласовании со последующим методом:
- найти т — 1 — наибольший показатель степени в представления числа по форме (4.1) для основания q;
- целочисленно поделить начальное число (Z10) на основание новейшей системы счисления в степени т — 1 (т.е. qm—1 ) и отыскать остаток от деления; итог деления обусловит первую цифру числа Zq;
- остаток от деления целочисленно поделить на qm-2 , итог деления принять за вторую цифру нового числа; отыскать остаток; продолжать эту последовательность действий, пока показатель степени q не достигнет значения 0.
Продемонстрируем действие метода на той же задачке, что подверглась рассмотрению выше. Найти т — 1 можно или методом подбора (50 = 1 < 123; 51 = 5 < 123; 52 = 25 < 123; 53 = 125 > 123, как следует, т — 1 = 2), или логарифмированием с оставлением целой части логарифма (log5123 = 2,99, т.е. m — 1 = 2). Дальше:

Методы перевода Zp_→ Z10 очевидно вытекает из представлении (4.1) либо (4.2): нужно Zp представить в форме многочлена и выполнить все операции по правилам десятичной математики.