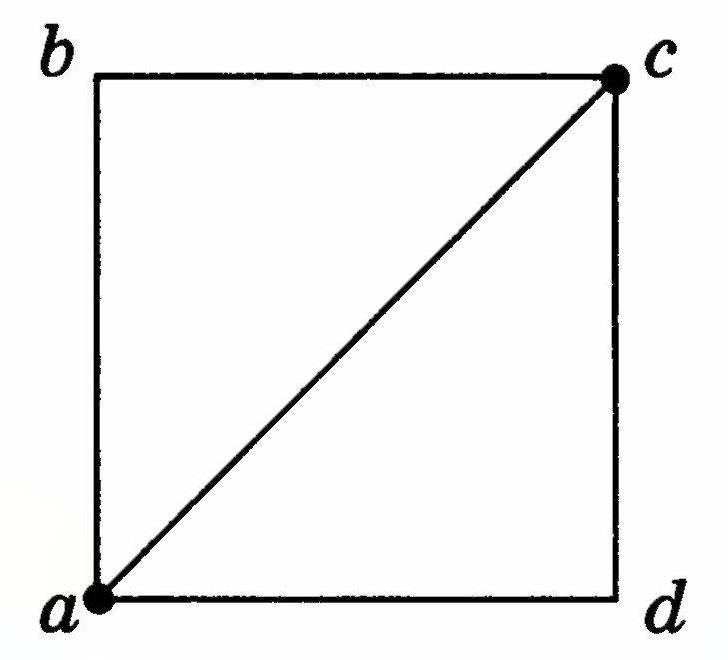
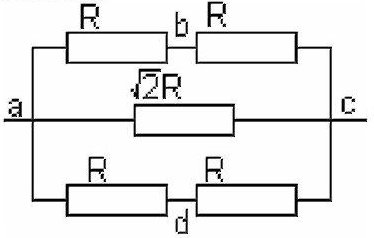
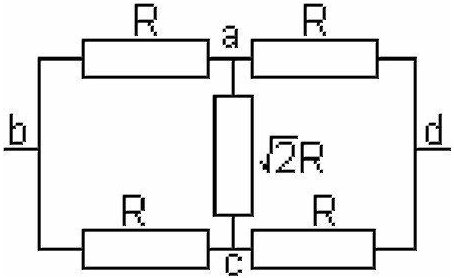
Сопротивление стороны проволочного квадрата равно R. Найдите сопротивления Rac,Rad,Rcd.

Дано:

R

Rac, Rad, Rbd — ?

Решение:

Сопротивление между точками а и с по теореме Пифагора равно R√(2).

Общее сопротивление R_ac легко сосчитать, заменив сперва последовательно соединенные резисторы сопротивлениями 2R, а потом параллельно соединенные оставшиеся резисторы.

1/Rac = 1/2R + 1/2R + 1/R√(2) = (2 + √(2))/2R ⇒ Rac = R√(2)/(1 + √(2))

Преобразуем схему квадрата так, как показано на рисунке. Дальше полученную схему легко преобразовать: 2R и R√(2) соединены параллельно, заменим их на:

R1 = 2√(2)R²/2R+R√(2) = 2R/√(2) + 1

R₁ соединено последовательно с R, их можно заменить на:

R2 = 2R/(√(2) + 1) + R = (R√(2) + 3)/√(2) + 1

Тогда эквивалентное сопротивление:

Rad = ((R√(2) + 3R)/(√(2) + 1))R/((R√(2) + 3R)/(√(2) + 1))+R = (R√(2) + 3R)/(2√(2) + 4)

Если рассматривать схему на рисунке 2, то через сопротивление ас ток идти не будет, а следовательно его сопротивление равно нулю (схема симметрична, то есть произведения сопротивлений противоположных плечей равны). Значит сопротивление: R√(2) — можно выкинуть из цепи.

Дальше заменим последовательно соединенные резисторы на их эквиваленты 2R, которые соединены параллельно. Таким образом Эквивалентное сопротивление цепи R_bd = R.

Ответ:

Rac = R√(2)/1+√(2), Rad = R√(2) + 3R / 2√(2) + 4, Rbd = R.