Геометрия Евклида как математическая система ничего не говорит о мире, в котором мы живем. Такая система теорем может быть самосогласованной и верной, а может оказаться противоречивой и ошибочной независимо от свойств реального мира, подобно тому как в шахматах невозможность поставить мат черному королю с помощью белого коня и-короля не зависит от того, сделаны ли конь и король из слоновой кости в традиционном стиле или выполнены из стали в современной манере.
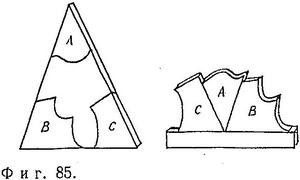
Тем не менее утверждение, что геометрия имеет определенное отношение к реальному миру, довольно наглядно. Рассмотрим треугольник (фиг. 85). Если отрезать его углы А, В и С и сложить их вместе, то мы обнаружим, что они образуют прямую, или угол в 180°.
Мы получим этот результат каждый раз, сколько бы треугольников мы ни вырезали из куска картона. Следовательно, можно высказать очевидное утверждение, касающееся свойств нашего мира и состоящее в том, что если нарисовать на куске картона треугольник, затем вырезать его углы и сложить их вместе, то они образуют прямую линию, т. е. линию, которая параллельна краю линейки. В этом смысле теорема «Сумма углов треугольника равна 180°» имеет прямое отношение к реальному миру.
Мы можем сделать геометрию физической системой, указав, каким образом реализуются в нашем мире те «неопределяемые объекты» теории, которые так смело, но не совсем успешно пытался определить Евклид. Необходимо договориться, какой смысл мы вкладываем в понятия точки и прямой линии. Как позже прозорливо отметил Ньютон, этот вопрос сам по себе не является геометрическим. Он пишет:
«Геометрия не учит тому, как проводить эти линии, но предполагает выполнимость этих построений. Предполагается также, что приступающий к изучению геометрии уже ранее научился точно чертить круги и прямые линии; в геометрии показывается лишь, каким образом при помощи проведения этих линий-решаются разные вопросы и задачи. Само по себе черчение прямой и круга составляет также задачу, но только не геометрическую».
Построения точки и прямой не являются задачами геометрии. В геометрии предполагается, что объекты (точки и прямые) заданы и обладают свойствами, определяемыми постулатами. Если в реальном мире можно реализовать такие объекты, то, поскольку они удовлетворяют правилам, соответствующие теоремы геометрии тоже будут выполняться.
Следовательно, когда мы говорим о геометрии как о физической системе, мы подразумеваем, что нами реализованы объекты, которые можно назвать точками, и объекты, которые называются прямыми (фиг. 86), причем эти объекты удовлетворяют геометрическим постулатам. Например, две точки можно соединить только одной прямой.
Теперь геометрия будет обладать свойствами физической теории. Между введенными таким образом объектами выполняются соотношения, справедливые в геометрии: сумма углов треугольника равна 180° и сумма квадратов катетов в прямоугольном треугольнике равна квадрату гипотенузы.
Наиболее тонким вопросом такой теории является ее интерпретация: каковы связи между объектами реального мира и «неопределяемыми объектами» математической системы? Как доказать, что этот объект обладает свойствами прямой линии, а это сооружение — свойствами треугольника? В случае геометрии такая интерпретация довольно очевидна. Но в более сложных физических теориях вопрос о связи между абстрактными объектами математического мира и соответствующими объектами реального мира является наиболее трудной проблемой принципиального характера.