Классическая планета, на которую действует гравитационная сила со стороны Солнца, вечно движется по эллиптической орбите, в одном из фокусов которой расположено Солнце. Если на планету подействует возмущающая сила, скажем вблизи нее пролетит комета, то орбита планеты изменится; если известны положения и скорости как кометы, так и планеты в какой-то момент времени, то можно вычислить их последующие траектории. В квантовой теории такие расчеты не только являются невозможными, но и не представляют особого интереса. Квантовый электрон, на который действует кулоновская сила со стороны атомного ядра, находится в одном из разрешенных состояний, определяемых решением уравнения Шредингера для случая атома водорода (1S, 2Р, …), и при отсутствии возмущения остается вечно в этом состоянии. Если же на электрон действует возмущающая сила (со стороны других атомов, электронов, протонов и т. д.), то его волновая функция будет так изменяться со временем, что это изменение можно будет истолковать как переход электрона в другое разрешенное состояние атома водорода. В квантовой теории обычно рассчитывают вероятности таких переходов.
[В этой связи удобно ввести определение движения аристотелевского типа. Полезно рассматривать движение планеты по эллиптической орбите или стационарную волновую функцию электрона как некое нормальное (или естественное при данных условиях) движение, которое происходит без внешнего воздействия. При включении внешнего воздействия (внешнего влияния, или возмущения) «нормальная» эллиптическая орбита или атомное состояние водородного типа могут измениться. Поэтому основной интерес представляет изучение «возмущений», способных вызвать переходы из одного состояния в другое.]
В классическом случае основная проблема механики состоит в следующем: где находится частица в момент t, если в момент t=0 ее положение и скорость были заданы? В квантовой же механике часто интересуются таким вопросом: если в момент t=0 система находится в каком-то «начальном» состоянии, то какова вероятность нахождения ее в каком-то другом «конечном» состоянии в более поздний момент времени t (фиг, 172)?
Рассмотрим квантовую систему, волновая функция которой при t=0 имеет какой-то определенный вид ψ(t=0). [В случае атома водорода ψ(t=0) может быть волновой функцией, соответствующей, например, 2P-состоянию системы. Тогда можно утверждать, что при t=0 вероятность нахождения атома в 2Р-состоянии равна единице, а вероятности нахождения атома в других состояниях равны нулю.] В квантовой динамике мы не рассматриваем движение электрона по орбите вокруг ядра. Мы не только не в состоянии это сделать, но нам это и не требуется. Нас интересует лишь изменение волновой функции со временем. Если на атом действует какое-либо возмущение, скажем электромагнитное поле (фотоны), то волновая функция в более поздний момент времени t будет отличаться от начальной волновой функции. Оказывается, что волновая функция типично квантовой системы становится со временем смесью (суммой, или суперпозицией) волновых функций, соответствующих различным состояниям системы, например, различным состояниям водородного атома.
Если, скажем, система находится в возбужденном состоянии и существуют два уровня, на которые эта система может перейти, то расчет вероятностей перехода между первым уровнем и двумя более низкими можно сравнить с интенсивностью соответствующего излучения. Если вероятность перехода между возбужденными уровнями 3 и 2 меньше, чем вероятность перехода между уровнями 3 и 1 (фиг. 173), то число атомов, совершающих переход 3→2, или число излученных фотонов с энергией Е3—Е2, будет меньше числа фотонов с энергией Е3—Е1,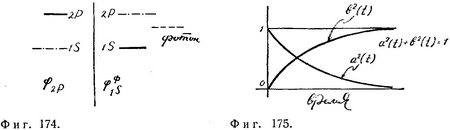
В качестве простого примера рассмотрим квантовую систему, которая обладает только двумя уровнями, или просто ограничимся рассмотрением лишь двух уровней определенной атомной системы, скажем уровней 2Р и 1S атома водорода. Волновую функцию водородного атома в состоянии 2Р обозначим следующим образом:
ϕ2P = волновая функция водородного атома в 2Р-состоянии, (44.6)
а волновую функцию системы, состоящей из атома водорода в состоянии 1S и излученного с соответствующей энергией фотона, — так (фиг. 174):
ϕФ1S = волновая функция водородного атома в
1S-состоянии и фотона с энергией hv = Е2P – E1S.
При t=0 волновая функция системы совпадает с волновой функцией водородного атома в 2Р-состоянии; в этот момент времени вероятность нахождения атома в 2Р-состоянии равна единице и вероятность нахождения атома в 1S-состоянии с испущенным фотоном равна нулю. Таким образом, при t=0 волновая функция системы:
ψ(t=0) = ф2P). (44.8)
Через некоторое время волновой функцией системы становится сумма волновых функций 2Р- и 1S-состояний с испущенным фотоном:
ψ(t) = α(t)ф2Р + b(t)ϕФ1S. (44.9)
Коэффициенты α(t) и b(t) характеризуют вероятности нахождения системы соответственно в 2Р- и 1S-состояниях. Так, при t=0 α(t)=1, a b(t)=0. С течением времени b(t) возрастает, a α(t) уменьшается (фиг. 175). Величина b(t) интерпретируется как амплитуда вероятности перехода между 2Р- и 1S-состояниями с излучением фотона. Величина же b2(t) есть вероятность перехода между этими двумя состояниями.
Обычно вероятность перехода между двумя уровнями отличается от нуля. (Все, что может случиться, рано или поздно произойдет.) Метод получения простых оценок величины вероятности будет дан позже. Если эта величина точно равна нулю, то соответствующий переход называется запрещенным. Как правило, невозможность перехода связана с каким-нибудь законом сохранения. Таким образом, классические законы сохранения проявляются в квантовой теории как условия разрешенных или запрещенных переходов. В рассмотренном выше случае, например, вероятность перехода отлична от нуля только в том случае, если энергия фотона в точности равна разности энергий уровней 2Р и 1S (сохранение энергии). При различных процессах вероятности перехода не равны нулю только тогда, когда такие величины, как энергия, импульс и угловой момент, сохраняются (их значения одинаковы в «начальном» и «конечном» состояниях). Какая же из величин сохраняется в том или ином случае, зависит от характера действующих сил и определяется, как мы видели раньше, симметрией системы. Таким образом, по виду разрешенных переходов, так же, как и по структуре вырождения квантовой системы, можно судить о свойствах симметрии соответствующей силовой системы. Например, если угловой момент не сохраняется (его величина различна в «начальном» и «конечном» состояниях), то можно заключить, что силовая система не остается неизменной при поворотах.