Используя введенные понятия, рассмотрим теперь одну из древнейших наук, статику, описывающую поведение твердых тел, которые не изменяют состояния своего движения. Она применяется при конструировании мостов, зданий и военных машин еще со времен по крайней мере Архимеда. В статике изучаются неподвижные твердые тела.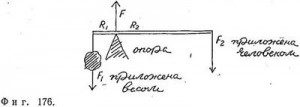

Это означает, что сумма сил, действующих на каждую частицу тела, равна нулю. Центр масс системы из N частиц находится в покое, если результирующая внешних сил, действующих на систему, отсутствует. Полный угловой момент системы не изменяется, если сумма моментов внешних сил равна нулю. Однако и при этих условиях система может колебаться или изменять свою форму другим способом. Ситуация существенно упрощается, если система — абсолютно твердое тело, ибо такая система может только двигаться поступательно или вращаться как целое. Следовательно, если суммы сил и моментов сил, действующих на твердое тело, равны нулю, т. е. если:

F^внешн = 0 (14.16)

T^внешн = 0 (14.17)

то тело будет либо равномерно вращаться, либо равномерно перемещаться, либо оставаться в покое. Возможность записать условия равновесия в виде только двух уравнений отражает существенные упрощения, связанные с введением понятия абсолютно твердого тела; эти условия эквивалентны утверждению, что сумма всех сил, действующих на каждую частицу твердого тела, равна нулю.

Сказанное можно изобразить в виде логической схемы: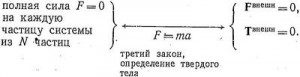

Пример. Использование рычага для подъема тяжелых предметов. Допустим, что сам рычаг не имеет веса. Тогда (фиг. 176)

F=F₁+F₂

(это уравнение само по себе не представляет интереса, пока мы не пытаемся выяснить, насколько прочной должна быть опора);

F₂R₂ – F₁R₁ = 0 (T^внешн = 0)

Отсюда

F₂ = (R₁/R₂)*F₁ (величина)

Если, например, R₁=30 см, а R₂=300 см, то человек может поднять груз весом 50 кг (~490 Н), действуя силой 5 кг (~49 Н). Человек мог бы поднять земной шар с помощью рычага достаточной длины. Инженеры, занимавшиеся строительством мостов и военных сооружений, были знакомы с этими и многими другими результатами задолго до Ньютона: эти результаты составляли один из разделов механики, известный еще Архимеду и Аристотелю. Когда Аристотель говорит о теле, вес которого в 10 раз больше веса другого, производящем в 10 раз больший эффект, возможно, он имеет в виду равновесие тел или то, что равновесие тел достигается при определенном отношении длин плечей рычага. Нам удалось получить эти результаты, используя различные свойства движения, начиная с постулатов Ньютона, подобно тому как Евклид объединил все известные до него факты в единую геометрическую систему.