Обычно автоматом именуют устройство, выполняющее без конкретного роли человека определенную последовательность операций, в итоге которой происходит преобразование вещественных объектов, энергии либо инфы. Когда говорится «без роли человека», то предполагается отсутствие очевидного управления со стороны человека в процессе выполнения операций. Но по сути управление осуществляется, но опосредованно, через программку, составленную за ранее человеком и заложенную в устройство. В предстоящем ограничим себя обсуждением только тех устройств, которые созданы для автоматического преобразования инфы, представленной в дискретной форме.

Так как устройство обменивается информацией с наружной средой, разумеется, оно должно владеть входным каналом, по которому информация поступает в него, также выходным каналом, через который выдается итог преобразования. Кроме этого, устройство может владеть памятью, в какой фиксируется его текущее состояние; итог обработки в общем случае определяется входными воздействиями и внутренним состоянием устройства. Будем считать, что для представления входной инфы употребляется некий конечный алфавит X (входной алфавит), а для представления выходной — конечный алфавит Y (выходной алфавит). Как отмечалось ранее, требование конечности алфавитов является следствием конечности времени обработки инфы. Внутренние состояния устройства также образуют дискретный набор, который можно считать внутренним алфавитом — будем обозначать его Q. Что касается числа разных внутренних состояний, то пока не будем делать относительно его никаких догадок.

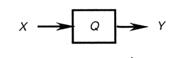
Будем считать также, что поступление входных знаков и переключение состояний устройства происходят не беспрерывно, а в определенные моменты времени, т.е. дискретно. Если последовательность моментов произвольна, то молвят об асинхронной организации работы частей устройства, к примеру, набор номера телефона либо кода замка. Но в сложных устройствах почаще употребляется синхронная организация, при которой моменты поступления и выхода сигналов, также переключения внутренних состояний следуют вереницей через один и тот же фиксированный просвет времени ∆t = const, именуемый тактом. Эти моменты задаются при помощи специального устройства — тактового генератора (либо генератора синхроимпульсов). Число тактовых импульсов за единицу времени именуется тактовой частотой — она является одним из важных причин, определяющих быстродействие устройства. Можно ввести моменты времени t₀, t₁, t₂,…, обозначающие границы тактов (t₀ соответствует моменту начала работы). При всем этом можно считать, что действия, относящиеся к такту i — поступление входного знака, изменение внутреннего состояния, формирование и выдача выходного знака — проистекают одномоментно в момент t_i.

Устройства, у каких дискретны огромного количества внутренних состояний, входных и выходных сигналов, также огромное количество моментов времени, в которые поступают входные сигналы, изменяются внутренние состояния и выдаются выходные сигналы, именуются дискретными.

Примерами дискретных устройств являются наборный диск телефона, кодовый замок, калькулятор, электрические табло и, непременно, компьютер. По предназначению устройства можно соединить в три группы:

• информационные — справочные автоматы, электрические табло, светофоры, устройства аварийной сигнализации и пр.;
• управляющие — кодовый замок, устройство управления лифтом, станки с программным управлением, процессоры фотоаппарата, видео и пр.;
• вычислительные — микрокалькулятор, процессоры компов.

Есть устройства, осуществляющие деятельность всех 3-х видов, к примеру, компьютер, автопилот и др.

Для наших рассуждений значимым оказывается то событие, что знаки на выходе и внутренние состояния такового устройства оказываются дискретными функциями входных знаков и номеров тактов работы. Введем понятие функции переходов Y, которая будет связывать внутреннее состояние устройства на следующем такте с состоянием и входным эмблемой на текущем такте:

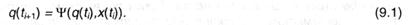
Другими словами, функция переходов указывает, в какое состояние из всех вероятных Q перейдет дискретное устройство, если оно находилось в состоянии q_i, а на вход поступил знак x_i.

Схожим же образом введем функцию выходов Q, которая будет связывать внутреннее состояние устройства и входной знак на текущем такте с выходным сигналом на этом же такте:

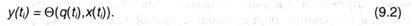
Как следует, функция выходов определяет, какой знак появляется на выходе, если на данном такте определен знак на входе и состояние устройства.

Молвят, что пятеркой компонент <Х, Y, Q, Ψ, Θ> задается автомат, обеспечивающий преобразование по определенным правилам последовательностей знаков входного алфавита в выходную последовательность. Вправду, если принять изначальное условие q₁ = q₀, то рекуррентные соотношения (9.1) и (9.2) обусловят порядок преобразования конечной последовательности входных знаков x₀, x₁ …, x_n в некую последовательность выходных знаков той же длины у₀, y₁,….y_n; при всем этом будет появляться определенная последовательность внутренних состояний q₁, q₂, … . В этом и заключается функционирование автомата. Выходной знак, вырабатываемый автоматом на неком такте i, зависит не только лишь от входного знака, воспринятого на этом же такте, да и от знаков, поступивших ранее — они фиксируются в автомате методом конфигурации его внутреннего состояния. В этом смысле огромное количество внутренних состояний автомата является его внутренней памятью. Зависимо от объема этой памяти выделяются последующие типы автоматов:

• без памяти;
• с конечной памятью;
• с нескончаемой памятью.

Забегая несколько вперед, заметим, что автомат с конечной памятью именуется конечным автоматом. Отметим также, что функции переходов и выходов имеют обобщающее заглавие автоматные функции.

Что касается дискретных устройств с нескончаемой памятью -это чисто модельное теоретическое представление, так как никакие реальные устройства нескончаемой памятью владеть не могут. Примером автомата с нескончаемой памятью может служить машина Тьюринга, в какой, как указывалось в п. 7.3.3, роль памяти делает нескончаемая (либо по мере надобности наращиваемая) в обе стороны картонная лента. Таким макаром, можно считать, что автоматом с нескончаемой памятью является метод, представленный в форме машины Тьюринга. Так как вопросы, связанные с функционированием машин Тьюринга уже рассматривались ранее, в данной главе они дискуссироваться не будут.

В реальных дискретных устройствах сигналы и их преобразования могут иметь различную физическую природу (электронную, механическую, пневматическую и пр.). Но от этой природы можно отвлечься и учить только общие законы построения автоматов и правила, определяющие преобразование инфы ими. Такие автоматы именуются абстрактными. В теории абстрактных автоматов решаются несколько групп заморочек:

• во-1-х, выясняется, какие преобразования вероятны в автомате, как их обрисовать, как выполняемые преобразования связаны с числом состояний (т.е. сложностью) автомата, есть ли неразрешимые автоматом задачки;
• во-2-х, исследуются эквивалентные преобразования автоматов; задачка эквивалентного преобразования состоит в построении автомата эквивалентного данному, но имеющего другое количество состояний (обычно, наименьшее);
• в-3-х, рассматривается круг вопросов, в каких определяется строение автомата по нраву и соотношению входных и выходных сигналов (автомат — «черный ящик») — это принципиальная прикладная задачка технической диагностики устройств, без которой невозможна их практическая эксплуатация;
• в-4-х, выделяются структурных частей автоматов и определяются правил построения из их сложных устройств (задачка синтеза автоматов) — с этим связана разработка новых автоматов, а именно, компов.

Принципиальным для практики личным случаем являются автоматы, в каких вся информация представлена при помощи двоичного кода, т.е. алфавиты X, Y и Q являются двоичными — такие автоматы именуют двоичными либо логическими. Последнее заглавие обосновано тем, что, как указывает теория, при двоичном кодировке хоть какой конечный автомат можно представить в виде композиции некого числа частей, реализующих логические операции И, Либо, НЕ, также элементы памяти (задержка и триггер). Объединение частей именуется логической схемой. Необходимыми представляются два происшествия: во-1-х, работу логических схем можно обрисовать законами и правилами математической логики (т.е. итог деяния логической схемы сводится к вычислению значения логического выражения); во-2-х, из данного маленького набора частей можно выстроить хоть какой конечный автомат.