За время между Кеплером и Ньютоном научная мысль в Европе значительно развилась. Кеплер придумывал невидимые спицы, которые соединяли Солнце с планетами и влекли их по орбитам; Тихо Браге отрицал теорию Коперника, так как Земля, по его мнению, была слишком массивна, чтобы когда-либо прийти в движение. Люди не могли понять, почему, если Земля перемещается, они не ощущают этого движения. Во время же Ньютона сформировался новый взгляд на проблему движения тел. В дискуссиях по этой проблеме большая часть усилий была направлена теперь на отыскание закона сил, действующих между Солнцем и планетами, из которого получались бы найденные Кеплером орбиты планет.
Место старого вопроса: «Как движутся планеты?» занял новый: «Почему они остаются на своих орбитах?». Массивность планет скорее мешает им остановиться, чем начать двигаться; к этому времени уже было признано, что естественное движение тел — это равномерное движение Декарта и Галилея. Постепенно созрело убеждение, что существуют какие-то законы, которые управляют движением тел и остаются справедливыми как на Земле, так и на небе. А может быть, эти же законы управляют движением планет? Если это так, то какие именно силы вынуждают планеты двигаться по кеплеровским орбитам?
Попытка объяснить движения небесных тел с помощью правил, основанных на земных наблюдениях, была сопряжена с определенным риском. Успех такой попытки можно расценивать как одно из величайших достижений науки семнадцатого века. В 1687 г. Ньютон опубликовал свои «Начала», в которых он разработал систему, описывавшую движения планет и в сущности любые другие движения чрезвычайно детально. С тех пор его имя стало неразрывно связано с этим монументальным и, впервые, строгим взглядом на мир как механическую систему, или машину, правила работы которой нам известны и чье поведение поэтому можно проследить, предсказать или проконтролировать, опираясь на эти правила.
Ньютон начал свои исследования движений планет с изучения орбиты Луны. Орбита Луны практически круговая, поэтому все связанные с ней расчеты относительно просты. Если бы на Луну не действовала никакая сила, она двигалась бы прямолинейно (первый закон); однако Луна обращается по окружности вокруг Земли. Следовательно, если верить первому закону, к ней приложена какая-то сила, действующая, возможно, между Землей и Луной. Ньютон пишет:
«…без такой силы Луна не могла бы. удерживаться на своей орбите. Если бы эта сила была меньше соответствующей ее орбите, то она отклоняла бы Луну от прямолинейного пути недостаточно, а если больше, то отклоняла бы ее более, чем следует, и приблизила бы ее от орбиты к Земле».
Какова в таком случае природа силы, заставляющей Луну обращаться вокруг Земли? Гораздо позднее Ньютон рассказал Генри Пембертону, с которым он часто беседовал на закате своей жизни, что однажды, раздумывая над этой проблемой, он увидел падающее яблоко и, пораженный этим, погрузился:
«…в размышления о мощи силы тяготения, которая не обнаруживает малейшего уменьшения даже в наиболее удаленных местах от центра Земли, куда мы в состоянии подняться: ни в верхних этажах самых высоких зданий, ни на вершинах высочайших гор; тогда он подумал, не разумно ли допустить, что действие этой силы распространяется гораздо дальше, чем обычно думают, скажем, до самой Луны. А если так, то сила тяготения должна оказывать влияние на ее движение, более того, может быть, именно она удерживает Луну на орбите».
В то время было известно, что ускорение яблока и любого другого свободно падающего предмета вблизи поверхности Земли, обусловленное ее притяжением, приблизительно равно 980 см/с2. Может быть, Луна тоже свободно падающее тело, но находящееся от Земли так далеко и движущееся так быстро, что, «падая», оно никогда не попадает на Землю и в результате вращается по стационарной орбите? Поэтому интересно было выяснить, совпадает ли ускорение Луны с ускорением предметов непосредственно вблизи земной поверхности.
Вычисление ускорения Луны
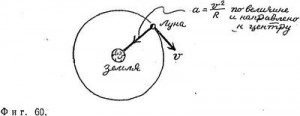
Луна, двигаясь с постоянной скоростью вокруг Земли, испытывает ускорение, направленное к центру вращения (как и любое тело, вращающееся с постоянной скоростью вокруг центра). Величина ускорения, как мы уже выяснили, равна v2/R (фиг. 60). Так как Луна удалена от Земли на расстояние примерно 384 000 км и обращается вокруг нее за 27,3 суток (2,36*106 с), ускорение Луны составляет:![]()
что гораздо меньше величины 980 см/с2, характеризующей ускорение тел, свободно падающих вблизи Земли.
Из этого грубого расчета видно, что ускорение Луны гораздо меньше того ускорения, которое она испытывала бы, находясь около поверхности Земли. Из этого можно было бы заключить, что сила, с которой Земля притягивает тела, уменьшается при их удалении, либо предложенный закон движения вообще неверен и непригоден на больших расстояниях порядка расстояния между Землей и Лупой или применительно к таким огромным телам, как Луна. Ведь этот закон был выведен по существу на основании весьма ограниченных наблюдений. С другой стороны, можно было допустить, что второй закон движения выполняется всегда, а полученное значение для ускорения Луны объясняется изменением величины силы.
Ньютон выбрал последнее предположение; много лет спустя он разъяснил, что закон сил был получен им с помощью обращения третьего закона Кеплера. Он допустил, что Солнце притягивает каждую планету с такой силой, которая как раз и удерживает ее на орбите, и что характер этого притяжения каким-то образом сходен с характером притяжения Луны Землей. В результате ему удалось, используя правило Кеплера о постоянстве отношения квадрата периода обращения к кубу радиуса ее орбиты для всех планет:
получить закон изменения силы притяжения с расстоянием.
Нельзя сказать, что эти предположения высказывал один Ньютон. Они витали в воздухе; думается, что Гук, Рен, Галлей и все остальные образованные ученые того времени были в принципе готовы совершить то же открытие.