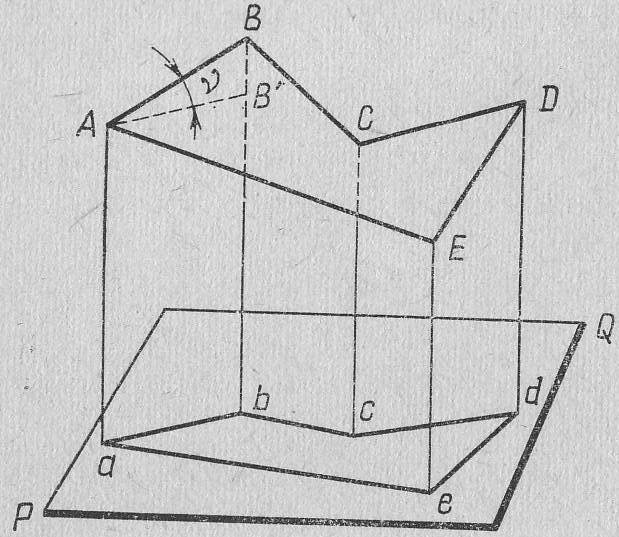
Пусть многоугольник ABCDE (рис. 2) представляет часть земной поверхности. Возьмем плоскость PQ и опустим из каждой вершины многоугольника перпендикуляр на эту плоскость. Основания этих перпендикуляров обозначим соответственно через a, b, с, d, е. Полученные на плоскости точки называются ортогональными (прямоугольными) проекциями точек пространства; линии ab, bс, … называются ортогональными проекциями линий АВ, ВС, … а углы abc, bcd, … — ортогональными проекциями углов АВС, BCD, … . Плоский многоугольник abode является ортогональной проекцией пространственного многоугольника ABCDE.

Рис 2. Ортогональная проекция

Другая имеющая весьма важное значение в геодезии проекция называется центральной.

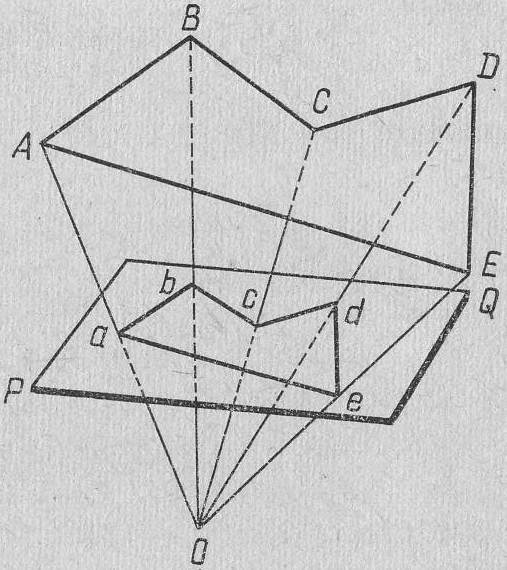
Суть ее заключается в следующем. Возьмем произвольную точку О (рис. 3) и соединим ее со всеми вершинами многоугольника АВСDЕ, находящегося на земной поверхности. Полученные в пересечении с горизонтальной плоскостью PQ точки аbcde и будут центральными проекциями точек АВСDE.

Рис 3. Центральная проекция

Плоский многоугольник abcde называется центральной проекцией многоугольника АВСОЕ.