Далее Клаузиус показал с помощью абстрактных и труднодоступных, как и все в физике, рассуждений, что можно определить такую функцию S, которая зависит лишь от параметров системы (например, от давления и температуры в случае газовой машины, но не от способа, с помощью которого были достигнуты такие значения температуры и давления) и изменение которой связано с количеством тепла, вводимого в эту систему. (Рассуждения Клаузиуса сходны с теми рассуждениями, с помощью которых мы доказали, что в случае консервативных сил потенциальная энергия зависит лишь от начального я конечного положений частицы, но не от формы пути, по которому она двигалась.)

Рассуждения Клаузиуса в наиболее простой форме выглядят так. Рассмотрим величину:

переносимое тело/температура

Процессы, происходящие в идеальной машине, изображены на фиг. 372.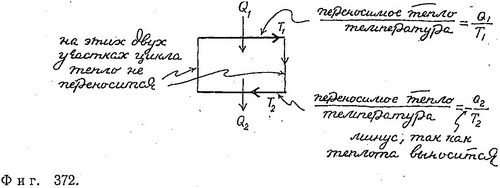

Для полного цикла:

Клаузиус показал, что этот результат не зависит от конкретной конструкции машины (скажем, от того, работает ли машина при двух температурах или при нескольких) при условии, конечно, что трение отсутствует. Отсюда он заключил, что значение величины:

вычисленной между двумя произвольными точками α и b (фиг. 373), не зависит от формы пути, а определяется лишь положением точек α и b. Эту функцию α и b Клаузиус назвал энтропией.

По поводу названия «энтропия» Клаузиус писал:

«Я предпочитаю обращаться к древним языкам в поисках названий для важных научных величин с той целью, чтобы эти названия обозначали одно и то же на всех живых языках. Поэтому я предлагаю назвать S энтропией тела, что по-гречески означает «превращение». Я специально так подобрал слово энтропия, чтобы оно было созвучно со словом «энергия», так как эти две величины настолько сходны по своему физическому значению, что созвучие их названий кажется мне полезным».

Поступив таким образом, Клаузиус не употребил для обозначения этой функции какое-нибудь известное выражение (скажем, теряемое тепло); тем самым ему удалось ввести слово, которое ни у кого не вызывает никаких ассоциаций.

Когда мы будем описывать теплоту и температуру с помощью механических понятий, таких, как полная энергия, средняя скорость, мы найдем очень простую и естественную интерпретацию понятия энтропии. Однако в данный момент любая формула может только запутать дело. Ибо главное сейчас состоит не в ее интерпретации, а в том, что такая функция существует и что она может послужить основой для формулировки весьма глубокого принципа.

Мы можем определить энтропию (как и энергию) для любых систем и для всей Вселенной. Функцию, введенную Клаузиусом, можно определить не только для паровых машин, но и для топлива, снабжающего теплом машины, для топки, где это топливо сгорает, для платформы, на которой стоит топка, наконец, для солнечной системы и для всей Вселенной, содержащей нашу солнечную систему. Согласно закону сохранения энергии, полная энергия Вселенной остается постоянной независимо от того, является ли Вселенная молодой или старой, измеряем ли мы энергию до или после рождения сверхновой звезды, до или после вхождения кометы в солнечную систему и т. д. Принцип, связанный с энтропией (эквивалентный второму началу термодинамики), состоит в следующем: энтропия всегда возрастает. В любом физическом процессе полная энтропия системы всегда увеличивается, хотя энтропия отдельных ее частей может при этом уменьшиться. Подобно тому, как утверждения, что для замкнутой системы 1) E =1/2 mv²+V+ электрическая энергия + … и 2) Е есть постоянная величина, являются математическим описанием принципа, согласно которому энергия не может возникать из ничего и не может уничтожаться, так и утверждения Клаузиуса, что для замкнутой системы 1) можно определить функцию S (энтропию) и 2) эта функция К растет в любом физическом процессе, являются математической формулировкой другого принципа, в соответствии с которым невозможно получить работу только за счет охлаждения тела до температуры, меньшей температуры окружающей среды¹⁾.

1) Охладить тело до температуры, меньшей температуры окружающей среды, можно (например, с помощью холодильника), но для этого необходимо совершить работу, т. е. иметь какой-нибудь двигатель.

Примененный ко всей Вселенной, этот принцип определяет направление течения любого физического процесса. Рост энтропии означает, что нагретые тела должны охлаждаться (все тела стремятся достичь температуры окружающих предметов) до тех пор, пока Вселенная в целом не израсходует все свое тепло, — тогда энтропия достигнет максимума и ничего больше произойти не сможет.

Был ли этот вывод причиной пессимизма Генри Адамса? В это трудно поверить.