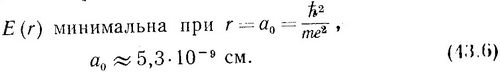Энергия основного состояния. Фундаментальное свойство любой замкнутой квантовой системы состоит в том, что лишь определенные значения ее энергии являются разрешенными; в отличие от классического случая спектр энергии такой системы дискретный. В классической теории наинизшее значение энергии системы электрон — протон соответствует состоянию, при котором электрон совмещается с протоном и покоится. В этом случае его кинетическая энергия равна нулю, а потенциальная обращается в минус бесконечность. В квантовой же теории дело обстоит по-другому, и мы теперь знаем несколько объяснений такого поведения квантовой системы. Например, используя принцип неопределенности, можно показать, что, пытаясь точно совместить положение электрона с положением протона, мы тем самым вносим большую неопределенность в величину его скорости, а это проявляется в увеличении кинетическом энергии электрона.

Для того чтобы проиллюстрировать, как на деле реализуются подобные квантовомеханические идеи, выведем еще раз с помощью простых рассуждений энергию основного состояния атома водорода. Полная энергия электрона, вращающегося по круговой орбите вокруг протона, равна:

Используя соотношения де Бройля:

и предполагая, что электрон находится на наинизшей орбите (n=1), получаем:

В результате наинизшая энергия системы окажется функцией лишь расстояния между электроном и протоном:

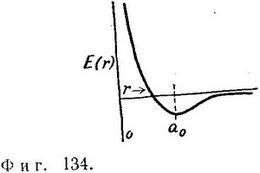
Этот результат резко отличается от соответствующего классического выражения, в которое импульс и расстояние входят совершенно независимым образом, так что (это мы уже отмечали ранее) минимальное значение энергии получается при р=0 и r=0. В квантовой теории это невозможно. Между р и r существует связь: при стремлении r к нулю член, описывающий потенциальную энергию в (43.5), становится, как и раньше, бесконечно большой отрицательной величиной, однако член, характеризующий кинетическую энергию системы, при этом возрастает, причем быстрее первого члена. Поэтому при уменьшении r полная энергия возрастает; при стремлении же r к бесконечности она становится очень маленькой, отрицательной величиной (фиг. 134). Энергия минимальна в какой-то точке α₀. Координату этой точки, где энергия минимальна, можно вычислить. Если бы мяч катался во впадине, по форме, совпадающей с кривой на фиг. 134, то он остановился бы в конце концов именно в этой точке. Оценить величину α₀ можно с помощью аккуратного графика. Результат вычисления α₀ имеет вид:

Это расстояние, при котором энергия минимальна, определяет так называемый Боровский радиус атома водорода, равный 5,3*10^-9 см. Далее, минимальная энергия равна:

что в точности совпадает со значением энергии атома водорода в основном состоянии. Чтобы ионизовать атом, т. е. оторвать электрон от протона, необходимо затратить энергию именно 13,6 эВ.

Может показаться удивительным, что с помощью таких простых расчетов нам удалось вычислить энергию основного состояния атома водорода; конечно, не все проблемы так просты. Однако использованные нами приемы составляют основу чрезвычайно общего и мощного метода решения задач квантовой теории. Этот метод опирается на тот факт, что основной квантовый уровень системы соответствует минимальному значению энергии системы.