Структурные схемы системы. Систему автоматического регулирования можно представить типовыми динамическими звеньями и изобразить на схеме. Схема системы автоматического регулирования, в которой все элементы или их составные части представлены типовыми динамическими звеньями, называют структурной схемой системы. Графически на структурной схеме каждое типовое динамическое звено системы изображают прямоугольником, а существующие связи между ними — стрелками, соответствующими направлению прохождения сигнала. Над стрелками пишут символы, обозначающие операторные изображения сигналов.

Структурные схемы, как и функциональные, отражают процессы передачи и преобразования информации. Однако функциональные схемы, как известно, характеризуют систему по составу входящих в нее элементов, которые рассматриваются с точки зрения их значения, тогда как структурные схемы определяют динамические свойства системы.

Структурные схемы системы автоматического регулирования составляют путем выделения динамических звеньев таким образом, чтобы для них можно было наиболее просто определить передаточные функции. В качестве примера составим структурную схему системы автоматического регулирования частоты вращения двигателя постоянного тока (см. рис. 25, б), функциональная схема которой изображена на рис. 26, б. Система состоит из задающего элемента — потенциометра П, полупроводникового усилителя У, электро-машинного усилителя ЭМУ, двигателя постоянного тока М, являющегося объектом регулирования, тахо-генератора Тг — элемента главной обратной связи.

Запишем выражения передаточных функций звеньев структурной схемы:

• усилителя — Wy(р)   = k_yΔU (p)/ΔU(р), где k_y — коэффициент усиления усилителя; по своим динамическим свойствам полупроводниковый усилитель является безынерционным звеном;
• электромашинного усилителя – W_эму = U_я (p)/k_yΔU (р) = k_эму/(Т_ур + 1), где k_эму – коэффициент усилителя ЭМУ; Т_у — постоянная времени обмотки управления ЭМУ; по своим динамическим свойствам ЭМУ является инерционным звеном;
• двигателя постоянного тока—W_д(p) = Ω(p)/U_я(р) = k_д/(T_дp + 1) р, где k_д — коэффициент пропорциональности частоты вращения двигателя величине напряжения на якоре; Т_д — электромеханическая постоянная времени двигателя с учетом инерции нагрузки; по своим динамическим характеристикам двигатель представляет собой передаточную функцию последовательно соединенных инерционных и интегрирующего звеньев;
• тахогенератора — W_Тг (р) = U_Тг (р)/Ω(p) = k_Tг, где k_Тг — коэффициент пропорциональности между напряжением на якоре и частотой вращения тахогенератора; по динамическим свойствам тахогенератор является безынерционным звеном.

На рис. 35 показана структурная схема системы автоматического регулирования частоты вращения двигателя.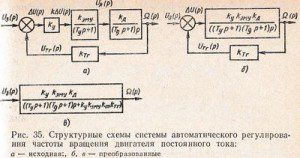

Соединение динамических звеньев и их передаточные функции. Систему автоматического регулирования можно представить в виде отдельных динамических звеньев на структурной схеме. Зная передаточные функции звеньев, можно найти выражение для передаточной функции системы, что важно при исследовании ее динамических свойств. Звенья, входящие в состав структурной схемы системы, могут быть соединены между собой последовательно, параллельно и встречно-параллельно.

Последовательным называют такое соединение звеньев, при котором выходная величина предшествующего звена является входной величиной для последующего (рис. 36, а). При последовательном соединении звеньев передаточная функция системы равна произведению передаточных функций этих звеньев: W(р) = W₁(p) W₂ (p) … W_n(Р).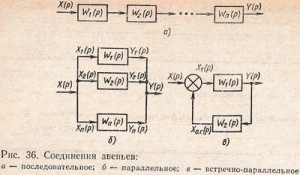

Параллельным называют такое соединение звеньев, при котором входная величина у всех звеньев общая, а выходные величины суммируются (рис. 36, б). При параллельном соединении звеньев передаточная функция системы равна сумме передаточных функций звеньев: W(р) = W₁(p) + W₂(p) + … + W_n(p).

Встречно-параллельным называют такое соединение двух звеньев, при котором выходная величина первого звена подается на вход второго, а его выходная величина суммируется с общей входной величиной и подается на вход первого звена. В этом случае образуется замкнутая система автоматического регулирования (рис. 36, в). Выражение для передаточной функции имеет следующий вид: W(р) = W₁(p)/[1 ± W₁ (p)W₂(p)], где знак «+» в знаменателе соответствует отрицательной обратной связи, а знак «—» — положительной обратной связи.

В качестве примера определим передаточную функцию системы автоматического регулирования частоты вращения двигателя постоянного тока, структурная схема которой показана на рис. 35, а. Звенья, охваченные обратной связью с передаточными функциями W_у(р), W_эму(p), W_д(р), соединены последовательно. В этом случае передаточная функция разомкнутой системы: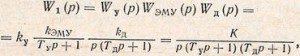

где К = k_уk_эмуk_д —коэффициент усиления системы.

Разомкнутая система с передаточной функцией W₁(р), охваченная отрицательной обратной связью, и звеном с передаточной функцией W_Tг(р) соединены встречно-параллельно. Следовательно, передаточная функция замкнутой системы:

На рис. 35, б, в показаны преобразованные структурные схемы системы.