Задачку увеличения чувствительности измерительного преобразователя можно решить за счет использования нелинейных процессов в сложных динамических системах (рис. 15.7). Коэффициент передачи такового измерительного канала находится в зависимости от реализуемых режимов связанных колебаний в системе. В итоге перераспределения колебательной энергии меж взаимодействующими осцилляторами процесс измерительного преобразования будет нелинейным, что можно использовать, к примеру, для сотворения высокочувствительных датчиков, применимых для измерения малых величин, для регистрации слабеньких воздействий и т.п.

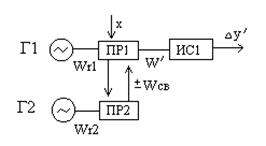
К примеру, режимы связанных колебаний в системах с конечным числом степеней могут быть реализованы в измерительных преобразователях, построенных на базе 2-ух взаимодействующих меж собой пьезорезонаторов (Рис. 15.7б).

а)

б)

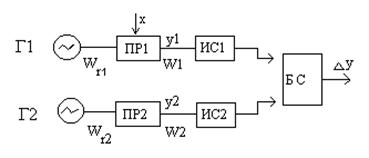
Рис. 15.7 Структурные схемы дифференциальных измерительных устройств линейного (а) и нелинейного (б) типов: Г- генератор; ПР – преобразователь; ИС – измерительная схема.

Связанные колебания в датчиках такового типа могут быть реализованы конкретно снутри цельных пьезорезонаторов, меж отдельными резонаторами, также на базе взаимодействия волн в системах с распределенными параметрами.

Неувязка понижения чувствительности преобразователей такового типа по отношению к дестабилизирующим факторам может быть также решена за счет оптимального использования соответственных режимов связанных колебаний в системе. В отличие от дифференциального способа выделения разностного сигнала, заключающегося в использовании дополнительного измерительного преобразователя и блока сопоставления сигналов(БС) (рис. 15.7а), формирование и усиление разностного сигнала при реализации режимов связанных колебаний осуществляется конкретно в самос преобразователе, в критериях наибольшего приближения к объекту измерения (рис. 15.7б).

В первый раз измерительный преобразователь, реализующий режим связанных колебаний, а конкретно – синхронный режим, был сотворен в США в 1932 году. К истинному времени режимы связанных гармонических колебаний отыскали применение в разных областях науки и техники. К примеру, с внедрением СВЧ-генераторов были реализованы многофункциональные преобразователи, в том числе и измерительные устройства. В текущее время используют в главном синхронные режимы связанных колебаний электронных контуров, генераторов с целью усиления принимаемого радиосигнала, сложения генерируемых мощностей, деления частоты гармонических колебаний, измерения электронных и неэлектрических величин и т.п. Есть публикации об использовании взаимодействующих оптических квантовых генераторов, СВЧ-волн, как в измерительных, так и в технологических установках. К примеру, на базе измерения разности фаз синхронизированных электронных колебательных контуров реализован высокочувствительный фазогенераторный способ измерения характеристик радиоэлементов. На базе взаимосвязанных генераторов разработаны многофункциональные преобразователи вида аналог-фаза и аналог-частота. Но, невзирая на достигнутые довольно высочайшие метрологические свойства, разработанные устройства с внедрением связанных колебаний широкого внедрения в технике не отыскали, может быть, это обосновано последующими причинами:

• недостаточно изучены и проанализированы режимы связанных колебаний, что не позволило воплотить рациональные схемные и конструктивные решения при разработке измерительных устройств;
• в качестве взаимодействующих осцилляторов применялись низкостабильные, сложные и дорогостоящие устройства (СВЧ-генераторы, электромеханические резонаторы, электронные колебательные контуры).

К примеру, по разным причинам режиму биения колебаний с частичным увлечением частот по сей день не уделено достаточного внимания как в плане теоретических и экспериментальных исследовательских работ, так и в плане практического внедрения.

Есть определенные различия в подходах к использованию связанных колебаний в разных областях инженерной деятельности. К примеру, при использовании режимов связанных колебаний в радиотехнических устройствах энтузиазм представляют в главном вопросы, связанные с определением размера полосы синхронизма, крутизны амплитудно-частотной свойства на границах полосы синхронизма, внедрением возможности колебательной системы к модуляции колебаний, сложению мощностей синхронизированных генераторов.

При использовании связанных колебаний в измерительной технике приходится решать ряд специфичных задач, связанных с улучшением метрологических черт измерительных устройств данного типа. При всем этом акцент делается на решение последующих вопросов:

• исследование способностей по увеличению чувствительности измерений за счет реализации режимов связанных колебаний;
• методы увеличения точности измерительных устройств, основанных на использовании связанных колебаниях в сложных системах;
• методы управления рабочими чертами ИП на связанных колебаниях;
• обеспечение стабильности работы сложных колебательных систем измерительных преобразователей.

Как проявили проведенные исследования и опыт практической реализации измерительных устройств данного типа, микропроцессорная обработка выходных характеристик позволяет значительно сделать лучше метрологические и технико-экономичес­кие свойства пьезоэлектрических преобразователей, основанных на модуляции связанных колебаний, расширить область их внедрения.

Математическая модель измерительного преобразователя с 2-мя степенями свободы

В текущее время резонансные способы измерения обширно употребляются в измерительной технике. Для этой цели в большинстве случаев реализуют автоколебательные процессы в системах различной физической природы. Развитие теории автоколебаний связано с именами Л.И. Мандельштама, Н.Д. Папалекси, А.А. Андронова, Н.М. Крылова, Н.И. Боголюбова, Ю.А. Митропольского и др. Значимый вклад в развитие теории автоколебаний и синхронизированных систем занесли К.Ф. Теодорчик, М.И. Конторович, И.С. Тодоровский, П.С. Ланда.

Процессы в автоколебательных системах описываются нелинейными дифференциальными уравнениями, в связи с чем почти всегда может быть только приближенное решение таких уравнений. При всем этом вводятся те либо другие допущения зависимо от особенностей колебательной системы и задач, которые ставятся при исследовании. Существует ряд способов подхода к анализу процессов в автоколебательных устройствах. Но при всем обилии проведенных исследовательских работ динамических процессов в сложных колебательных системах по сей день не разработаны теоретические базы сотворения пьезоэлектрических измерительных устройств с внедрением связанных колебаний.

Конструктивно такие устройства могут состоять из 1-го цельного пьезоэлемента, 2-ух и поболее пьезорезонаторов, в том числе и составных, а в качестве элемента акустической связи меж взаимодействующими степенями свободы может выступать измеряемая среда. При всем этом необходимо учесть то, что электромеханический резонатор является системой с распределёнными параметрами, в какой могут возбуждаться разные моды колебаний и типы связи меж ними. Эквивалентная электронная схема замещения таких устройств имеет непростой вид и может состоять из огромного числа взаимодействующих меж собой контуров.

В связи с тем, что процессы в автоколебательных системах описываются нелинейными дифференциальными уравнениями, почти всегда может быть только приближенное решение таких систем уравнений. При всем этом вводятся те либо другие допущения зависимо от особенностей колебательных систем и задач, которые ставятся при их исследовании. Потому существует ряд способов подхода к анализу динамических процессов в автоколебательных устройствах.

В разработанных к истинному устройствах такового типа употребляются режимы синхронизации, биения колебаний с частичным увлечением частот, бифуркационные процессы. В качестве выходного сигнала датчиков употребляются, к примеру, отношение либо разность амплитуд, фаз, частот связанных колебаний.

Исследование режимов работы преобразователя такового типа как системы чисто нелинейной и неконсервативной является довольно сложной задачей. Зависимо от вида нелинейной свойства колебательной системы, уровня наружного гармонического воздействия, соотношения частот будут наблюдаться разные результирующие эффекты. Коэффициент передачи акустического тракта (коэффициент акустической связи) также является сложной функцией и находится в зависимости от степени поглощения звука в среде, ослабления плотности потока звуковой энергии, обусловленной расхождением волн при излучении и рассеянием при отражении. Нужно учесть также запаздывание сигнала в акустическом тракте элемента связи (ЭС).

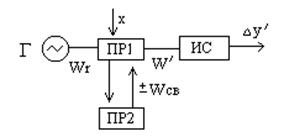
Для описания устройства и механизма работы таких средств измерений комфортно представить пьезорезонансный датчик, реализующий режимы связанных колебаний, в виде облегченной эквивалентной схемы замещения (рис. 1.4).

Рис. 15.8 Структурная (а) и эквивалентная электронная (б) схемы замещения преобразователя: АГ – автогенератор; ПР – пьезорезонатор; ЭС – элемент акустической связи

При анализе режимов работы датчика комфортно представить его колебательную систему в виде 2-ух связанных электри­ческих контуров, возбуждаемых в режиме автоколебаний (рис. 15.8). Измеряемая физическая величина при всем этом может модулировать характеристики контуров и элемента связи. Исследование режимов работы датчика такового типа сводится к анализу математической модели колебательной системы с 2-мя степенями свободы.

Уравнения колебаний для 2-ух связанных контуров, возбуждаемых в режиме автоколебаний, могут быть представлены в виде(15.1):

где х – безразмерная переменная;

n – собственная частота колебательного контура;

m – малый параметр, характеризующий близость данной системы к линейной;

F(x) – функция, определяющая нелинейность колебательного контура;

g – коэффициенты связи (g1 – емкостной, g2 – индуктивной и g3 – диссипативной составляющих).

Для анализа режимов связанных колебаний в системе с малой диссипацией и малой нелинейностью (колебания не достаточно отличаются от гармонических) применяется способ медлительно меняющихся амплитуд. Потому что собственные частоты резонаторов близки, то решения уравнений имеют вид (15.2):

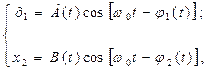 где А; B – медлительно меняющиеся во времени амплитуды колебаний;

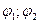– медлительно меняющиеся во времени фазы колебаний;

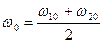– частота совместных колебаний.

При асинхронном режиме взаимодействия происходит противофазная модуляция амплитуд связанных колебаний с частотой биения (W) и глубиной модуляции (m), зависящей от соотношения коэффициентов связи (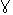), относительной расстройки частот контуров (x) и амплитуд (χ) колебаний (15.3):

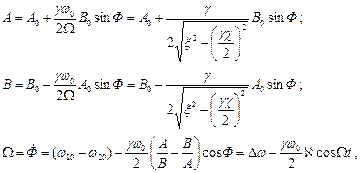
где 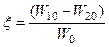– относительная расстройка частот; 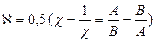– относительная расстройка амплитуд; 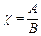– коэффициент рассредотачивания амплитуд колебаний; Ф – разность фаз связанных колебаний.

При анализе колебательных систем употребляют близкие по физической сути понятия, к примеру, для анализа синхронных режимов связанных колебаний – коэффициент связанности (σ), соотношение полуширины полосы синхронизма к относительной расстройке частот либо соотношение токов во взаимодействующих контурах.

В синхронном режиме вероятны два устойчивых режима синхронных колебаний: синфазный (a = 0) и противофазный (a = p). При всем этом формулу для дела амплитуд колебаний можно представить в виде (15.4):

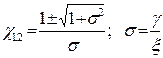
Коэффициент связанности (s) можно найти через парциальные частоты (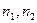) системы (15.5):

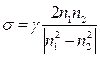
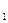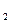На рис. 15.9 представлена АЧХ синхронизированной системы. Частоты ωи ωсоответствуют режимам синфазных и противофазных колебаний и могут быть найдены из выражения (15.6):

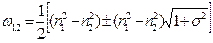
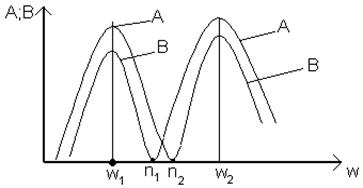
Рис. 15.9 АЧХ колебательной системы с 2-мя степенями свободы

При сильной связанности (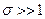) для дела амплитуд колебания на частотах (ω1) и (ω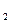) можно записать

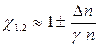
При доминировании упругой составляющей в коэффициенте связи частота синфазных колебаний (ω1), как понятно, больше частоты противофазных колебаний (ω):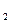

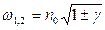
При доминировании инерционной составляющей, напротив, частота синфазных колебаний (ω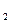) меньше частоты противофазных колебаний (ω):

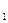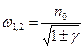
Таким образом, как надо из приведенных формул и графиков, при реализации синхронных режимов взаимодействия колебательных контуров в качестве выходного параметра измерительного устройства могут быть применены величины, пропорциональные отношению либо разности частот, фаз либо амплитуд связанных колебаний.

При реализации асинхронного режима связанных колебаний фазовый портрет системы с 2-мя степенями свободы имеет вид эпициклоиды либо гипоциклоиды зависимо от того, рассматривается ведущий либо ведомый контур. В режиме обычных биений взаимодействие меж контурами фактически отсутствует, потому биения колебаний происходят фактически по гармоническому закону. Режим биения колебаний с частичным увлечением частот характеризуется сложным видом огибающей колебаний взаимодействующих осцилляторов.

В режиме биения колебаний с частичным увлечением частот пульсации частоты и амплитуды колебаний сдвинуты на 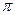/2 и имеют асимметричный вид. С приближением к полосе синхронизма асимметрия растет. Это приводит к повышению небаланса числа синфазных и противофазных колебаний за период биения колебаний, что, в свою очередь, сопровождается повышением глубины амплитудной модуляции до критичного уровня, а при предстоящем увеличении коэффициента взаимодействия происходит уменьшение амплитудной модуляции до нуля и вход системы в синхронизм.

При всем этом частота биений стремится к нулю, а период биения 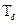и число колебаний за период биения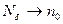при неограниченно растут (15.7):

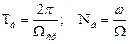
Парциальными подсистемами пьезорезонансных МСК датчиков могут быть взаимодействующие степени свободы цельных пьезоэлементов, отдельные пьезорезонаторы, составные пьезорезонаторы и вибраторы, электронные контуры, взаимодействующие через пьезоэлектрический элемент связи. Это определяет огромное обилие вероятных типов пьезорезонансных датчиков. Режимы взаимодействия осцилляторов зависят от нескольких переменных: коэффициента связи (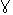); относительной расстройки частот (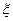); дела амплитуд колебаний (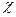). В связи с этим можно выделить три главных метода модуляции коэффициента взаимодействия, что обусловит три главных принципа реализации механизма чувствительности пьезорезонансных датчиков. Одним из их является воздействие измеряемым параметром (x) на элемент связи: .

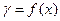К данной группе измерительных устройств можно отнести разные типы датчиков на взаимодействующих пьезорезонаторах с жидкостными, газообразными либо твердотельными элементами акустической связи. Достоинством такового принципа построения датчиков будет то, что измеряемое воздействие не прикладывается конкретно к высокодобротным осцилляторам, что обусловливает увеличение метрологических и эксплуатационных черт резонансных преобразователей.

2-ой принцип построения ПР датчиков состоит в том, что измеряемая физическая величина модулирует конкретно эквивалентные характеристики взаимодействующих степеней свободы таким макаром, что в итоге меняется их относительная расстройка частот: . Данный механизм чувствительности может быть рекомендован для измерения, к примеру, характеристик механических, термических и других воздействий.

Модуляция измеряемым параметром разности фаз связанных колебаний 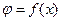может быть осуществлена, к примеру, при использовании элемента связи в качестве управляемой в функции измеряемой величины полосы задержки акустических сигналов. Особенный энтузиазм представляет реализация методов управления отношением амплитуд связанных колебаний 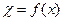. Модуляцию величины 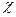можно производить последующими методами:

• воздействием на добротность осцилляторов;
• регулированием уровня возбуждения со стороны генератора;
• введением в колебательную систему дополнительного осциллятора.

При разработке конструкции датчиков одной из главных заморочек является понижение воздействия дестабилизирующих причин на результаты измерений. Для рассматриваемого типа датчиков увеличение точности и стабильности измерений может быть достигнуто за счёт:

• а) внедрения размеренных и высокодобротных пьезорезонаторов;
• б) реализации соответственных режимов работы МСК-датчиков;
• в) внедрения разных схемных решений, позволяющих создавать компенсацию воздействия дестабилизирующих причин.

При разработке ПР датчиков нужно найти рациональные значения характеристик резонаторов и элемента связи, обеспечивающие рабочий режим колебательной системы преобразователя. Основными аспектами при всем этом могут служить, как было показано ранее, последующие соотношения (15.8):

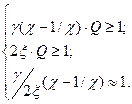
Определяющим фактором при разработке пьезорезонаторного датчика является значение акустического импеданса исследуемой среды. При использовании газовой среды в качестве элемента акустической связи нужно использовать высокодобротные пьезорезонаторы. Уменьшение при всем этом относительной расстройки частот взаимодействующих пьезорезонаторов (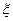) не нужно из-за растущего воздействия флуктуации частоты автогенераторов.

К примеру, при содействии пьезорезонаторов через воздух значение коэффициента связи должно быть в границах . При добротности кварцевых и пьезокерамических резонаторов, соответственно Q1 = 104 и Q2 = 102, нужно для выполнения условия (3.6) обеспечить отношение амплитуд колебаний: для пьезокварцевых резонаторов в границах χ=10, а для пьезокерамических – χ = 103. Потому для измерения газообразных сред можно советовать применение пьезокварцевых резонаторов. При содействии пьезорезонаторов через жидкость либо твёрдое тело может быть внедрение пьезокерамики с низкой добротностью, к примеру ЦТС-19, ЦТС-23 и т.п.

Относительная расстройка собственных частот пары резонаторов должна выбираться из условия (3.6). Для пьезокварцевых датчиков (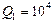) она может составлять значение 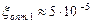, а для пьезокерамических (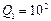) соответственно .

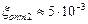С целью роста относительной расстройки частот датчиков можно использовать низкодобротные пьезокерамические материалы, но увеличение уровня взаимодействия меж пьезорезонаторами при газообразном элементе связи за счет роста коэффициента рассредотачивания амплитуд колебаний (χ) связано с повышением напряжения возбуждения пьезорезонаторов, что может привести к их перегреву, проявлению нелинейных эффектов в пьезоматериале и т.п.

Если в качестве элемента связи будет применена жидкость, то нужно согласовать с величиной механической добротности системы площадь акустического контакта меж пьезорезонатором и измеряемой средой, используя для этой цели переходные согласующие элементы. Вероятна также реализация пьезорезонансных датчиков на кратных и комбинированных частотах. Необходимость сотворения датчиков данного типа может быть обоснована необходимостью обеспечения высочайшей рабочей частоты преобразователя.

Особенный энтузиазм представляет возможность реализации режима модуляции связанных колебаний (радиально-изгибных, продольно-поперечных и т.д.) в измерительных преобразователях, представляющих из себя сложные колебательные системы.

Примеры конструктивного выполнения пьезорезонансных измерительных преобразователей, основанных на реализации связанных колебаний в системах с 2-мя степенями свободы

Режимы связанных колебаний могут быть реализованы в измерительных преобразователях, состоящих из цельных пьезоэлементов, акустически либо электрически связанных пьезорезонаторов (ПР), составных ПР и пьезоэлектрических трансформаторов (ПЭТ). Огромное обилие конструктивного выполнения датчиков определяется принципами реализации механизма чувствительности, критериями эксплуатации и рядом других обстоятельств. При всем этом можно выделить несколько главных вариантов конструктивного выполнения ИП. Как было показано при систематизации, датчики данного типа могут быть построены на базе 1-го цельного пьезоэлемента, снутри которого реализуются режимы связанных колебаний, либо с внедрением более сложных конструкций, состоящих из взаимодействующих вибраторов либо электронных колебательных контуров. Методики расчета и проектирования таких устройств значительно отличаются друг от друга.

Таким макаром, режимы связанных колебаний могут быть реализованы снутри цельных пьезоэлементов, в составных пьезорезонаторах, также меж акустически связанными электронными колебательными контурами и т.п. При всем этом в качестве выходного сигнала датчика, зависимо от требований к обеспечению точности измерений, могут быть применены как абсолютные значения характеристик связанных колебаний (амплитуда, фаза, частота, число колебаний), так и разность либо отношение сигналов.

На рис. 15.10 представлены варианты выполнения колебательной системы пьезорезонансных измерительных преобразователей с внедрением связанных колебаний, определяющие три главных конструктивных типа датчиков:

• а, б – ПР МСК-датчики, основанные на использовании связанных колебаний в цельных пьезорезонаторах;
• в, г, д – ПР МСР-датчики, реализующие процессы взаимодействия меж отдельными пьезорезонаторами;
• е, ж, з – ПР МСВ-датчики, реализующие волновые процессы в составных пьезорезонаторах.

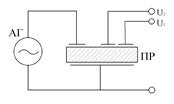
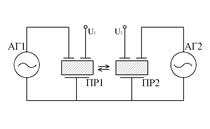
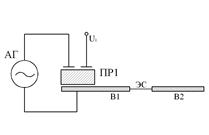
Рис.15.10 Варианты построения колебательной системы преобразователя: АГ – автогенератор; ПР – пьезорезонатор; В – вибратор; U1,U2 – выходные напряжения.