Для качественного понимания некоторых вещей, которые будут подробно рассмотрены позже, изучим поведение N частиц, взаимодействующих между собой по определенному закону, и допустим, что на одну из них действует внешняя сила; будем обозначать эту частицу буквой А. Возможны три случая:

• Частицы системы не взаимодействуют между собой (фиг. 142). (Считаем, что первоначально частицы покоятся.) Под действием внешней силы частица А начнет двигаться в направлении силы в соответствии со вторым законом Ньютона. На остальные частицы сила не действует, поэтому они, естественно, останутся на прежних местах. Позднее мы используем эту систему в качестве модели газа.
• Допустим, что все частицы соединены между собой слабыми пружинами, так что, если частицы смещаются из исходного положения, пружины сжимаются или растягиваются, оказывая сопротивление перемещению (фиг. 143). Под действием внешней силы частица А слегка смещается, как показано на рисунке, увлекая за собой остальные частицы, т. е. из-за наличия пружин исходная конфигурация частиц нарушается. Анализ такой системы, наиболее общей из всех трех, сопряжен с большими трудностями. В зависимости от жесткости пружин ее можно использовать в качестве модели жидких, желеобразных и эластичных тел.
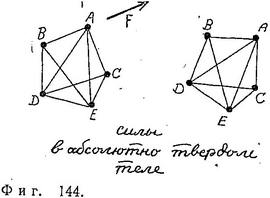
• Представим, что пружины стали настолько жесткими, что они ведут себя подобно стержням. В этом случае взаимное расположение частиц всегда сохраняется (фиг. 144). Иными словами, если частица С находится на расстоянии 2 см от частицы D, то она всегда будет находиться от D на таком же расстоянии. Если частицы А, В и С образуют треугольник с определенными сторонами и углами, форма и размеры его никогда не изменятся. Если на частицу А, как и раньше, подействует сила, она потащит вместе с А и все остальные частицы системы, причем взаимное расположение частиц внутри системы не изменится.

В рамках теории Ньютона невозможно установить, существуют ли подобные силы и какова их действительная природа, однако если допустить, что они существуют и являются ньютоновскими (т. е. подчиняются третьему закону), то окажется, что мы сможем существенно продвинуться в объяснении явлений природы. Когда мы попытаемся установить действительную природу этих сил, перед нами встанет целый ряд совершенно новых вопросов, для ответа на которые нам придется исследовать внутреннее строение вещества. Так происходит при пересечении различных направлений исследований, когда ответ на один вопрос порождает другие, представляющие не меньший интерес.

Хотя в дальнейшем мы будем изучать следствия именно третьей модели, которую используем для описания твердых тел (подобных стальной болванке), ясно, что любое физическое тело не может быть абсолютно твердым, а будет сгибаться или колебаться под действием силы достаточно большой величины. Поэтому мы сразу же можем заключить, что предположение абсолютно жестких связей между частицами недостаточно для полного описания поведения твердых тел. Тем не менее при таком допущении задача становится настолько простой, что мы принимаем его и рассматриваем все отклонения реальных сил от сил, соответствующих абсолютно жестким связям, как поправки к исходной идеализированной модели.

Успех такого подхода зависит от того, не окажутся ли эти поправки настолько большими, что они полностью изменят все качественные свойства исходной системы. Нетрудно проиллюстрировать это положение. Так, считая мяч круглым, мы знаем, что, если его внимательно рассмотреть, мы заметим на его поверхности различные неровности; однако разумно считать, что эти неровности малы по сравнению с общей округлостью. С другой стороны, мы могли бы описывать мяч для игры в регби тоже как шар, но при этом обнаружили бы довольно большие отклонения от формы шара; нетрудно догадаться, что, такое описание будет менее плодотворным, чем в первом случае.